|
|
| What Does "Software Is Mathematics" Mean? Part 2: A Semiotics Approach to the Patent Eligibility of Software by PolR |
 |
|
Thursday, November 29 2012 @ 07:05 AM EST
|
What Does "Software Is Mathematics" Mean? - Part 2
A Semiotics Approach to the Patent Eligibility of Software
by PolR
[This article is licensed under a Creative Commons License; article as PDF.]
I argued in part 1 of this series that computations are manipulations of symbols with meanings. In this article, I hope to further explain this notion using the social science of semiotics. Its object is the study of signs, the entities which are used to represent meaning.
This article elaborates on what Richard Stallman said in the recent Santa Clara Law conference Solutions to the Software Patent Problem.
According to this report Richard Stallman described patents on software as patents on thought, which amount to patents on the use of the human brain to reason and to solve problems by the application of reasoning. This article uses semiotics to show that Stallman's point is more than rhetoric. It is a provably correct statement of fact.
Professor Michael Risch
described two major currents of opinions
in the software patent debate. He calls one of these currents "utilitarians". These people believe that the costs of patenting might be worth the benefits of patenting. Or maybe they aren't, but that's the important question to them: to what extent does allowing software patent drive innovation? The other group is exemplified by Stallman. He doesn't believe software patents drive innovation, but this is not the important question to him. The real issue is whether the legal safeguards against the privatization of human understanding are working correctly. If not, then it doesn't matter whether software patents drive innovation. Privatization of human understanding is unacceptable as a matter of human rights.
There may be patents involving software which don't privatize human thoughts but the current interpretation of the law doesn't draw a meaningful line. The Federal Circuit in
CLS Bank International vs Alice Corporation
complained that no one understands what makes an abstract idea abstract.1 In this article I argue that semiotics is the correct framework to draw this line. The knowledge of semiotics let us distinguish when an advance over the prior art is an improvement in the human understanding as opposed to a new and nonobvious application of the physical properties of computer hardware.
In part 1, I argued that a test based on manipulation of symbols would correctly identify the abstract ideas in software. In this article, I will attempt to show how such a test could draw the line where it belongs according to semiotics. This should answer the questions asked by the Federal Circuit when they
granted en banc review of
CLS Bank vs Alice.
a. What test should the court adopt to determine whether a computer-implemented invention is a patent ineligible "abstract idea"; and when, if ever, does the presence of a computer in a claim lend patent eligibility to an otherwise patent-ineligible idea?
b. In assessing patent eligibility under 35 U.S.C. § 101 of a computer-implemented invention, should it matter whether the invention is claimed as a method, system, or storage medium; and should such claims at times be considered equivalent for § 101 purposes?
Summary of the Argument
[The article is based on the works of Professor Kevin Emerson Collins. See
Semiotics 101: Taking the Printed Matter Doctrine Seriously, Kevin Emerson Collins | 85 Indiana Law Journal 1379 (2010) (
PDF
).]
In semiotics, a sign is a sign when it has a semantics defined by conventions. Interpreting a sign according to the conventions is a faculty of the human mind. This faculty is what must be protected from privatization.
A sign has three components which must be distinguished. There is the sign-vehicle which is the physical occurrence of the sign. There is the referent which is the actual thing which is referred to by the sign. And there is the interpretant which is the idea a human interpreter would form in his mind when interpreting the sign according to its defining convention. For example marks of ink on paper forming the letters CAT are a sign-vehicle. The corresponding feline animal is the referent. The idea of a cat a human being may form in his mind is the interpretant. The combination of all three elements is the sign.
Programmed computers are sign-vehicles. The data stored in computers is defined by conventions which must be interpreted by humans. In part 1, I showed three examples of such conventions.
-
There are conventions which assign to voltages in wires a bit value 0 or 1. The same boolean gate doing the same electrical activity on voltages will perform either as an AND gate or an OR gate depending on which convention is used to interpret the voltages.
-
There are conventions on how series of bits read as numbers. The same arithmetic circuit manipulating bits in the same manner will perform different operations of arithmetic depending on whether the numbers are in unsigned or 2's-complement format.
-
There are conventions on which non mathematical meanings the numbers will stand for. The same arithmetic circuit will compute 1+1=2 or 1 apple + 1 apple = 2 apples or even 1 lawyer + 1 lawyer = 2 lawyers depending of the convention which is used.
This shows the functions of software are not performed through the sole physical properties of electrical circuits. The human mind plays a role because semantics is not built into the physical structure of the hardware. The functions of a programmed computer depends on the conventions used to interpret the data. This is like a clock. The clockwork is a patentable mechanical device but it cannot fulfill its functions without a convention on how to interpret the position of the hands.
This simple fact exposes one of the errors in the doctrine that programming a computer makes a new machine. In theory this doctrine purports to patent inventions whose functions are performed though the physical properties of electrical circuits. In practice it permits patents on interpretants. It is used to justify exclusive rights on thoughts and logical processes in the human mind.
If we choose to view a computer as a machine that processes electricity independently from the human mind there is no semantics. We only have meaningless electrical phenomenons like voltages, charges and currents. Programming a computer is not a nonobvious improvement over the prior art without semantics. Storing meaningless electrical charges in the capacitors of main memory is a well known procedure.
Programming a computer requires defining the data. The programmer must define the conventions on the syntactic organization of the bits and the corresponding semantics. Then he must define the operations of arithmetic and logic which will solve the problem. This is all interpretants. This is all thoughts in the programmers' minds.
Collins' article discusses how semiotics applies to software. In doing so he makes two errors. The first one is he accepts the doctrine that programming a computer makes a new machine. The second one is he considers only the point of view of the end user. He pays no attention to the point of view of programmers and computer engineers. He believes the information stored in the computer which is not visible to the end user does not have a semantics in the sense of semiotics. This is incorrect, Computer programmers routinely examine the internal states of computers with debugging tools. They interpret the meaning of the hidden data when doing so. Besides, the three example of conventions from above apply to all data whether or not it is visible to the end user. The internal state of a computer is a sign because it has a semantic meaning defined by human conventions.
The same conclusion may be reached from reading the words of a patent. The disclosure of a software patent typically requires the programmer to interpret the computer as a sign in order to reproduce the invention because the functions of the software are defined in terms of the meaning of the data. Also, when the claim recites the meaning of the data, we need to interpret the computer as a sign to determine infringement.
Once Collins' errors are corrected his article gives us a precise description of what is an abstract idea in software. If the invention is a sign and the only nonobvious advancements over the prior art are interpretants then the claim is directed to an abstract idea.
Summary of Part 1
Let's have a short recapitulation of part 1. This will refresh our memory before we move to the main topic.
Mathematical Algorithms Are Procedures for Manipulating Symbols
A computation is a manipulation of symbols conveying meanings. This manipulation is described by a procedure called an algorithm.
At the hardware level, stored program computers execute computations using a procedure called the instruction cycle. This procedure works as follows:
-
The CPU reads an instruction from main memory.
-
The CPU decodes the bits of the instruction.
-
The CPU executes the operation corresponding to the bits of the instruction.
-
If required, the CPU writes the result of the instruction in main memory.
-
The CPU finds out the location in main memory where the next instruction is located.
-
The CPU goes back to step 1 for the next iteration of the cycle.
As you can see, the instruction cycle executes the instructions one after another in a sequential manner. In substance the instruction cycle is a recipe to "read the instructions and do as they say".
This procedure manipulates symbols because it manipulates bits and bits are symbols.
This procedure is also an example of what is known in computation theory as a universal algorithm. This is a subcategory of algorithms mathematicians have found. Universal algorithms have the capability to compute every function which is computable. If we give this algorithm a program as input it will compute the corresponding function.
Several universal algorithms are used in computer programming. Some of them, like bytecode interpreters, are implemented in software. The most often used universal algorithm is the instruction cycle implemented in the hardware of every stored program computer. The notion that all computer programs are ultimately the execution of some universal mathematical algorithm is the factual basis of the slogan "software is mathematics".2
A Way to Design a Test to Identify Patent Ineligible Abstract Ideas
Mathematical algorithms are a subcategory of manipulations of symbols and manipulations of symbols are a subcategory of abstract ideas. I propose that the court should use a test based on manipulations of symbols to identify the abstract idea.
The basic principle is that a manipulation of symbols should be an easy to define concept. The Federal Circuit has found that terms like mathematical algorithm and abstract ideas are hard to define. But if we remove the definitional difficulty the biggest hurdle toward getting a workable test should be solved.
Details on how I believe the test should work will be found below in this article.
Some Elements of Semiotics
Semiotics is a social science dedicated to the study of signs. Law professor Professor Kevin Emerson Collins has suggested to use semiotics to reinterpret the printed matter doctrine as a sign doctrine. He says the printed matter doctrine actually curbs the reach of patent protection into mental representations in the human mind. According to Collins a semiotics approach is revealing both the conceptual coherence hidden in the printed matter doctrine's historical applications and the doctrine's as-of-yet unnoticed statutory grounding.3
The Triadic Notion of a Sign
Collins explains the basics of semiotics thus:4 (footnotes omitted, emphasis in the original)
Semiotics is the study of signs, and signs are entities that involve something standing for something else to somebody. To conceptualize the operation of a sign, Peirce and his followers posit a triadic model of the sign. They argue that every sign involves three distinct components: a sign-vehicle, an interpretant, and a referent.
The Peircean sign is commonly depicted as a triangle, as in Figure 2:
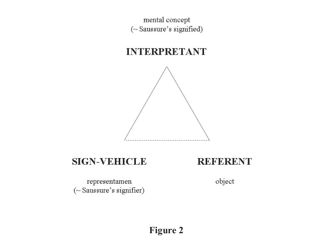
The sign-vehicle is the perceptible form of the sign; it is the physical artifact that an interpreter perceives. The particular combination of curves that make up the letter "S" and the formal properties of the dots, dashes, and blank spaces that make up a message transmitted in Morse code are both sign-vehicles, as are the undulating sound waves that convey the sound of the word "dog." The interpretant is roughly the concept that the sign-vehicle invokes in the mind of a person for whom the sign is meaningful. The referent of a sign is the thing in the world that is described, indicated, or referred to by a sign. Both interpretants and referents are within the ambit of the general term semiotic meaning as employed in this Article. For precision, a sign-vehicle will be described as signifying its interpretant and referring to its referent.
Peirce's sign "involves a rejection of the equation of 'content' and meaning; the meaning of a [sign-vehicle] is not contained within it, but arises in its interpretation" by an interpreter in the form of an interpretant. In other words, the sign-vehicle is not the sign, despite the commonplace nature of the language in which the material sign-vehicle is employed as a synecdoche for an entire sign. Stop-signs-as-artifacts -- the physical, red, octagonal things located at intersections -- are not signs in and of themselves. They are sign-vehicles and therefore only components of signs. The sign is the combination of the perceived thing (the sign-vehicle), the mental concept that the sign triggers in the mind of an interpreter (the interpretant), and the things or events in the world to which the sign refers (the referents). The sign-vehicle is a particularly useful term for the perceived component of the sign precisely because it wears on its sleeve a warning against the misleading synecdoche.
As you can see semiotics gives us the vocabulary to name with precision the constituent elements of a sign.
This triadic conceptions of signs is applicable to computer science and any other engineering discipline which involves computations. I think it is very insightful to see a sign not as a single indivisible entity but as a composite of constituent elements. It is also insightful to observe that an interpretant is an idea in the mind of the human interpreter. This is precisely the type of understanding we need to distinguish abstract ideas involving computations from concrete patent eligible inventions.
There is more on semiotics in Collins' article. If you are interested please read the whole article.
Signs Are Characterized by Social Conventions
In semiotics we must distinguish between causal relationships resulting from the action of physical phenomenons and semantical relationships resulting from social conventions. This distinction allows to recognize when something is a sign. Collins explains.5 (footnotes omitted)
Defined in the negative, a sign-vehicle is an entity that acquires meaning through a mechanism other than through deterministic cause and effect. It is "a physical phenomenon which provokes reactions in mechanisms and organisms, without being the cause of these reactions." The physical reactions provoked in interpreters by signs -- to the extent that there are any extroverted reactions at all by the interpreters -- are mediated by minds and mental states. In a positive manner, Eco defines semiotics to involve only the study of things that stand for other things by social convention. The key concept is that simply through a social agreement, the semiotic meaning of the stop sign can change.
Clearly, this distinction draws a boundary. We can apply it to the functions of computing machines such as programmable computers. On one side we have functions which are performed through the physical properties of the device. They involve some cause and effect relationships dictated by some laws of nature. On the other side we have functions which are performed through an operation of the mind of an interpreter. This operation associates meanings to sign-vehicles. It is defined by agreements between humans.
This boundary is one possible way to distinguish between abstract ideas and concrete inventions. Sometimes we may have a claim written to a sign-vehicle where the only nonobvious advancement over the prior art is the meaning of the sign. The innovation is entirely an understanding in the human mind, an interpretant. These claims are written to abstract ideas. Collins reinterprets the printed matter doctrine in this manner.
The data processing functions of a computer also lie on the semiotic and abstract side of the boundary. The evidence has been documented in part 1 of this series of articles. Let's recapitulate the main points. Please note how the meanings may change according to how humans define conventions. This is how we recognize when a sign is indeed a sign.
-
The first evidence is the ability of the engineer to decide whether a given voltage means the bit 0 or the bit 1. Depending on his decision the exact same circuit manipulating the exact same voltages will carry out a boolean AND or a boolean OR operation. The difference is not physical, it is in the perception of the engineer and it is controlled by a convention. In semiotic terms a bit is a sign with three components. The abstract symbol 0 or 1 is an interpretant, the voltage representing the bit is a sign-vehicle and the corresponding truth values and numbers are the referents.
-
When a circuit for addition adds 10000000+01111111 resulting into 11111111 it could mean either 128+127=255 in unsigned integer format or -128+127=-1 in 2s-complement format. At the physical level the same circuit manipulates the voltages in an identical manner. The difference is in the syntax the user has chosen to represent the numbers. This shows that one cannot reasonably argue the numbers are part of the physical structure of the computer. They are part of how human beings understand the activity of the computer. They are interpretants determined by the choice of a syntactic convention.
-
There is also the semantical relationship between bits and numbers on one side and the real world referent on the other side. This too isn't a physical property of electrical circuit. For example the difference between 12+26=38 and 12 apples + 26 apples = 38 apples isn't a difference in the physical properties of a calculating machine. It is a convention on how the numbers should be interpreted. Once again the association of numbers with real life things is a decision of a human.
In all of the three examples the exact same circuit doing the exact same electrical activity actually performs different functions depending on how the engineer or programmer choses to interpret it. This is the key. Semantical relationships are determined by social agreements. They are choices that may be changed. Humans would not have the option of changing these choices had the functions been performed through the physical properties of the circuit.
The Functions of Programmed Computers Depend on Human Understanding
The alternative view is to treat the computer as a machine for manipulating voltages in wires, electrical charges in capacitors and magnetic moment on hard disks. It will happily perform its functions whether or not someone is looking at the meanings of data. Think of an anti-lock brake system. The embedded computer will make the car brake without locking the wheels in absence of a human observer. In this sense the computer performs its functions according to the laws of physics.
This view omits semantics. We may defend it when the functions of the circuit don't require the physical phenomenons to have meanings. Otherwise we have three counterexamples: the interpretation of voltages in boolean gates, the representation of the syntax of numbers and the non mathematical meaning given to mathematical entities. These three examples cover the most fundamental element of computing: the representation of data. The functions of software depends on the knowledge of the conventions used to represent the data. This is not an physical property of an electrical circuit. In the three counterexamples we have the exact same circuit operating physically in an identical manner and they perform a different function when the conventions are changed.
Let's consider what happens when we introduce a program into a computer. The program itself is data. It is stored as electrical charges in capacitors located in main memory.6 Each charge represents a bit. Instructions are series of bits to the intention of the instruction cycle. The CPU will read these bits instruction by instruction and perform the corresponding operations.7 When viewed this way it is tempting to argue that the interpretant is irrelevant. The behavior of the computer is dictated by the physical properties of the electrical circuit. Collins actually defends this thesis:8
To understand the irrelevance of the interpretant, consider a hypothetical in which human understanding is taken out of the picture. Even if humans did not understand the genetic code, an isolated and purified gene would be patentable because it could be used to provoke a cell to produce a protein. Similarly, software on a disk is an advance over the prior art because its structure causes a computer to exhibit a particular behavior. Even if computer programmers forgot how to read and understand a programming language, the computer software recorded on a disk would remain patentable because it would still cause the machine to exhibit a specific behavior.
Let's see how this thesis works out in reality. Let's assume we have a program for managing reservation in a conferences. We received 128 reservations from the web site and 127 reservations through regular mail. The program contains an instruction to add the two numbers: it adds 128+127 for a total of 255 reservations. What is exactly the particular behavior of the computer while it executes this instruction, assuming the human understanding is taken out of the picture?
Without human understanding we don't know whether a particular voltage in a wire is the bit 0 or the bit 1 because this is defined by a convention which must be interpreted by a human. The circuit processes meaningless electricity. This is not performing the functions of software.
Let's ignore this point and assume we may see the computer as a machine for manipulating bits. Then, the instruction adds 10000000+01111111 resulting into 11111111. Without human understanding how do we know this is 128+127=255 instead of -128+127=-1? Electrically speaking this is the same machine behavior. The same adding circuitry processing the same bits will perform both additions depending on whether the programmer decided to use unsigned arithmetic or 2s-complement arithmetic. The instruction triggering this addition is exactly the same in both cases. The difference lies solely in the intent of the programmer.
Let's ignore the two preceding points. Without human understanding how do we know the numbers 128, 127 and 255 refer to reservations to a conference? How do we know they aren't a count of apples in a grocery inventory program? This knowledge is not built into the electrical structure of the machine. Once again there is no observable difference in electrical behavior.
The information processing functions of a computer cannot be separated from human understanding. A programmed computer is a sign and the computer hardware is a sign-vehicle. The thesis that interpretants are irrelevant to the computer behavior is not tenable when the behavior is defined in terms of manipulation of bits, numbers and logical operations on their meanings. Interpretants are irrelevant only when the behavior is defined in terms of meaningless physical phenomenons.
New Nonobvious Interpretants Are Patent Ineligible Abstract Ideas
The draftsmen of patents have a choice. They may describe the behavior of computers solely in meaningless electrical terms. Then interpretants are irrelevant to this purely electrical behavior. They may also describe the behavior in terms of data processing. Then the interpretants are relevant because they are recited in the patent.
If a patentee considers the computer as a machine for manipulating voltages can he patent it? Before answering this question I would ask, is there a nonobvious advancement in the manipulation of meaningless voltages? If so the claim must recite this advancement to be granted. If the only advancements over the prior art are interpretants,
the invention is an abstract idea in the mind of the interpreter.
An old fashioned mechanical clock may provide a good analogy. Put the clock in a dark room where nobody goes and it will keep time unattended. The clockwork performs its functions according to the laws of physics whether or not someone watches it. But time can only be read by a human interpreting the position of the hands. This is a semantical relationship.
The convention for reading time may be changed. This makes the clock a sign according to semiotics. For example, suppose we decide to use a decimal time system. In this system there are 20 hours in a day, 10 before noon and 10 after. Each hour is divided in 100 minutes and each minute is divided in 100 seconds. We can easily build a clock that keeps time according to this new system. We just have to paint the numbers 1 to 10 on the old clock in place of the old numbers. Then the position of the hands can be interpreted according to the new convention. The short handle indicates the hour and the long handle indicates the minutes if you mentally multiply the numbers by 10.
Here is the abstract idea question. Did we invent a new clockwork which performs its functions according to the law of physics? Or did we invent a new way to interpret the meaning of an old clock? Of course, in the decimal clock example the clockwork was not changed. The invention amounts to painting new numbers on the clock.
This is not inventing a new clock.
A programmed computer is like this clock. If we omit the semantic and consider only the physical properties of the circuit there is no new and nonobvious element in a programmed computer. The electrical circuit always carry out the instruction cycle. The program is electrical charges stored in main memory. There is nothing new and nonobvious in storing meaningless electrical charges in memory. Besides, the contents of memory is modified billions of times per second as the computation progresses. The configuration of main memory is a moving part of the machine. At the electrical level, then, programming the computer doesn't make a new machine.9
Programmed Computers Are Interpreted by Programmers
When debugging a program, a programmer will examine the data using debugging tools to verify its meaning. Software implements operations of logic. The software performs its functions only when the data manipulations are logically consistent. The task of debugging is to verify this is the case and correct any error.
There is an alternative view where the computer is a device for producing sign-vehicles. In this view, only the input and output visible to end users are signs. The internal states of computers are not considered to be signs because they are not visible to the end user. This view fails because it doesn't take into account that the internal state is visible to programmers. End users are not the only human beings able to interpret signs in a computer.
For a programmer, an unattended computer is like a book sitting on a shelf. This book isn't currently read but its meaning is available to whoever opens it. Similarly, no one checks the internal state of a programmed computer once the program is done debugging. But programmers know that if they inspect it they will read the meanings.10
The implication is that the internal activity of a computer is a sign even when it is not actually examined by a live human. This is the correct result. According to semiotics, a device is a sign whenever there is some convention on how to interpret its meaning. The requirement is not that someone actually applies the convention. It is that the convention must be defined. Then if someone comes along and uses the convention, the meaning could be understood.
Defining the conventions which make a programmed computer a sign is part of computer programming. The programmer defines how the data is represented and what is the semantics. The programmer defines the operations of arithmetic and logic the algorithm must carry out. The computer performs its functions precisely because the electrical activity of the computer is a sign-vehicle. This activity represents the correct operations of logic when the data is interpreted according to the conventions. When this is not the case, the software has a bug. It produces the wrong answer. The programmer must then inspect the internals of the computer to determine where the error is. This procedure requires him to analyze the semantics of the internal computer activity. In other words, the computer must be interpreted as a sign.11
This situation is typically reflected by the words of a patent. The disclosure mentions the data definition and the operations of arithmetic and logic. The implementer who follows the disclosure is required to interpret the computer as a sign. The claim similarly recites the data definition and the operations of arithmetic and logic. The computer must be interpreted as a sign when determining whether the claim is infringed.
The opposite view -- that there is no sign unless someone must actually watch the sign-vehicle -- leads to absurd results. A book sitting on the shelf would not be not a sign until it is opened and read. A DVD containing a movie picture would not be a sign because no one actually looks at the bits on the disk in their compressed format.12 Cuneiform tablets buried in the sands of the Mesopotamia would not have been signs during all these centuries where the ancient Sumerian language was forgotten.
The Courts Should Stop Using the "New Machine" Doctrine
According to a long-standing series of precedents, programing a computer makes a new machine distinct from the unprogrammed computer. I argue that this doctrine prejudges the outcome of the analysis which must be made. When the claim is directed to an abstract interpretant no new machine is made.
The courts have explained why they have adopted this doctrine in several ways. Here is how they explained it in
In re Noll (November 18, 1976),
There is nothing abstract about the claimed invention. It comprises physical structure, including storage devices and electrical components uniquely configured to perform specified functions through the physical properties of electrical circuits to achieve controlled results. Appellant's programmed machine is structurally different from a machine without that program.
We have just seen that this is false. Semantics is not a physical property of an electrical circuit.
Sometimes people argue that programming a computer makes a new machine because the functions of the computer are new. This argument takes for granted that the functions of software are performed through the physical property of the circuit. What if these functions are performed through conventions on how to interpret the meaning of the data? In such case the invention is an interpretant in the mind of the programmer. The machine is not changed just because we understand it differently.
The "new machine" doctrine is factually incorrect. Also, this doctrine precludes the conclusion that the invention could be an interpretant.
I protested that the "new machine" doctrine is technically erroneous in a preceding article. I have presented there several reasons why this doctrine is factually incorrect. I have also cited several cases where the courts have explained how they justify the "new machine" doctrine. All these explanations are based on erroneous interpretations of how a stored computer works. None of these explanations consider the role of semantics. They all assume the functions are performed as stated in Noll "through the physical properties of electrical circuits to achieve controlled results". We find more erroneous theories of this nature in the concurrent opinions of judges Rader and Newman in In re Alappat13 and also in an amicus brief submitted to the Supreme Court in Bilski v. Kappos.14
Lawyers say the "new machine" doctrine is a legal fiction.15 They say the courts understand programming a computer doesn't make a new machine. They say the courts don't mind making a legal fiction if they believe software is the type of invention which reasonably is within the scope of patent law and a fiction is necessary to achieve this result. In this case I wonder why the courts believe it is reasonable to patent software in the first place. All indications I could find say that the courts believe what is said in Noll: that the functions of software are performed through the physical properties of electrical circuits. No independent justification appears to exist.
To put it different way, why would an interpretant reasonably fall within the scope of section 101 of patent law? Here is how this section reads:
Whoever invents or discovers any new and useful process, machine, manufacture, or composition of matter, or any new and useful improvement thereof, may obtain a patent therefor, subject to the conditions and requirements of this title.
The courts should stop using the "new machine" doctrine. It purports to grant patents on electrical improvements of the unprogrammed computer when no such nonobvious improvement occurs. It is nothing more than an excuse to confer patent rights to ideas in the mind of programmers.
How to Identify Abstract Ideas in Software Patents Using Collins' Proposed Sign Doctrine
Collins has proposed to apply semiotics to the printed matter doctrine. He has analyzed the core printed matter cases. He found that all these cases could be reinterpreted as what he calls the sign doctrine.16 (footnote omitted, emphasis in the original)
When the printed matter doctrine is reconceptualized in a semiotic framework and recast as the sign doctrine, the core printed matter cases can be seen to follow a simple rule: a claim that describes a sign is not eligible for patent protection if the sole locus of the nonobvious improvement over the prior art resides in a mental state. Semiotically framed, what courts are already doing under the banner of the printed matter doctrine -- but not what they are saying they are doing -- is invalidating claims that describe a sign in which the only nonobvious advance over the prior art resides in the processes that occur in the minds of interpreters. It is the interpretant of a sign, not the content of information more broadly, that cannot be given patentable weight.
Collins further explains the procedure:17 (footnote omitted)
The key to distinguishing permissible claims to signs from impermissible ones is not to inquire whether the patent claim describes a sign-vehicle but rather to determine whether what is novel and nonobvious is the semiotic meaning that a human interpreter should understand when she perceives a sign-vehicle. The semiotic framework for patent eligibility, therefore, focuses the exclusion from patentable subject matter not generally on meaningful things but specifically on improvements in human understanding itself.
I argue that this logic also applies to software. Just to be clear, I do not argue the printed matter doctrine applies to software. I argue that abstract ideas in a computer program are abstract precisely because they are interpretants. Therefore it makes sense to follow this sign doctrine. I also argue the human interpreter need not be the user of the software. He may be a programmer, a computer engineer, anyone who attempts to reproduce the invention from the disclosure or even an expert witness analyzing the invention to determine infringement.
Collins argues his doctrine requires a
patentable-weight
approach because otherwise it is not possible to identify claims written to abstract ideas when the claim is written to a sign. On the other hand the courts prefer to use a
claim-as-a-whole
approach when analyzing section 101 subject matter. The difference is this. In a patentable-weight approach the claim is patent eligible only when there is a nonobvious advancement over the prior art outside of the interpretants. This requires to consider the novelty and obviousness of individual claim elements during section 101 analysis. But in a claim-as-a-whole approach novelty and obviousness must be left out of section 101 and deferred to the analysis of sections 102 and 103.
Collins solves this dilemma by narrowly limiting his proposed sign doctrine to signs. Then claims are still analyzed with the preferred claim-as-a-whole approach except in those limited circumstances where it doesn't work.
Collins explains:18 (emphasis in the original, footnotes omitted)
First, on a conceptual level, the semiotic framework explains why it is appropriate for the patentability of an artifact to hinge on the content of the prior art and thus the historical context in which an invention was made. There is no reason to expect patent eligibility to be an intrinsic property of an artifact in a semiotic framework. Semiotic meanings are not intrinsic properties of artifacts. Semiotic meanings are not contained within artifacts; sign-vehicles do not have "content" in the sense of meanings contained within them. Printed matter is meaningful only because of the mental process of interpretation in the mind of an interpreter. Signs, not sign-vehicles, are the entities within which meanings reside. If a single component of a sign is artificially cabined off from the sign's other components -- for instance, if the sign-vehicle is examined in isolation -- it should be unsurprising that its eligibility for patent protection depends on something other than that single component's intrinsic properties.
To understand the value of a patentable-weight approach to the doctrine of patent eligibility in the context of semiotically meaningful things, consider the absurd results of taking a claim-as-a-whole approach to patent eligibility seriously. In other words, consider a hypothetical sign-as-a-whole approach to patent eligibility. Under a sign-as-a-whole approach, courts would have to take note of all of the components of a sign -- the sign-vehicle, the interpretant and the referent -- every time an inventor claimed a sign. If any of those individual components described patentable subject matter, then the claim as a whole would describe patentable subject matter. Because every sign has a perceptible sign-vehicle that is an extra-mental thing, every sign would be eligible for patent protection under the sign-as-a-whole approach. Despite their insistence on a claim-as-a-whole approach to patent eligibility, courts have understandably never shown interest in a sign-as-a-whole approach. Such an approach would not reach normatively acceptable ends. Only a patentable-weight approach can effectively prevent the privatization of advances in human understanding.
This argument is applicable to software because a programmed computer is a sign. Software patents as they are currently granted privatize advances in human understanding. Collins' proposed sign doctrine would end this practice.
A Test For Patent Ineligible Abstract Ideas
I have proposed to design a test based on manipulation of symbols. I now argue that this test is a good way to apply the sign doctrine to software patents. A programmed computer is a sign because bits are symbols with meanings. An analysis of the manipulation of symbols will correctly identify software patent claims where the sole nonobvious improvement over the prior art are interpretants.
The test works in three steps. Together they ensure Collins' proposed sign doctrine is narrowly applied to signs as per his recommendation.
-
The first step identifies whether data, semantics and operations of logic or arithmetic are recited in the claim. If so the claim recites a sign and we go to the next step. Otherwise the sign doctrine is not applicable.
-
The second step identifies whether the claim is written to the sign as opposed to something which merely uses a sign as one of its elements. Insignificant element of the claim must be disregarded in this analysis in accordance to Parker vs Flook and Mayo Collaborative vs Prometheus. The claim is deemed to be written to the sign when the utility of the claim as a whole is the substantially same as the utility of the sign taken in isolation. The assumption is that significant elements will substantially alter the utility of the claim while insignificant ones will not. If the claim is written to a sign we go to the next step. Otherwise the sign doctrine is not applicable.
-
The third step is to apply Collins' proposed sign doctrine using a patentable-weight approach. The claim is patent eligible only if there is a new and non obvious advancement over the prior art outside of the interpretants.
I will now walk through how this test should work. I will show that this test accepts claims that should be accepted and rejects claims that should be rejected. I use an anti-lock brake system as an example. This invention comprises the following elements:
-
There are sensing devices which measure physical phenomena like the rotation of the wheels and the pressure the driver applies to the brake pedal.
-
These measurements are sent to a microprocessor programmed with the anti-lock braking software.
-
The microprocessor produces as output how much pressure must be applied on the wheels by the brakes.
-
This output is received by an actuator which applies the pressure on the brakes.
This invention is not mere pushing around of the bits. I have chosen it because I think it put the proposed test under the maximum stress.
Separating Causal Relationships from Semantical Relationships
The first step of the test would be to determine whether the claim recites a manipulation of symbols. Any recitation of data, semantics, arithmetic or logical operations or even a general description of the functions to be achieved by the software would meet the requirements of this test This is a threshold step. If there is no manipulation of symbols the test is not applicable. Otherwise we can move to the next step. In the case of the anti-lock brake system, the outcome of this step depends on how the claim is written.
In one scenario the patent may be written in a language which doesn't refer to bits, numbers or the meanings of data. It only mentions physical devices and meaningless electrical phenomenons like currents and voltages. Perhaps the microprocessor isn't a programmable device. Perhaps it is a dedicated circuit and the patent recites how to make the circuit by assembling electronic components. An engineer who wants to reproduce the invention from the patent disclosure doesn't need to consider the meanings of the bits. He may just assemble the components and make sure the electric currents and voltages are as specified. Similarly, an expert witness in a lawsuit will determine infringement by examining the physical structure of the device without having to look at the meaning of the bits.
A patent like this is clearly written to an application of the laws of physics. It depends solely on causal relationships. There is no mention of sign and interpretants. People are free to implement an anti-lock brake system where a different circuit carries out the same computation. The sign doctrine should not be applied in this case.
Another scenario would sound like some customer entering a bookstore asking "I want this book about a hobbit traveling in far away countries where live elves and orcs. He wants to destroy an evil ring." These words are not describing an arrangement of physical marks of ink on paper. This request is: "I want the book which tells the story I am outlining." This is asking for a sign-vehicle by specifying its meaning. The patent may be written in that style. It describes the meanings of numbers measured by the sensors. The functions of the algorithm are described in terms of the meanings of the data. An engineer who needs to reproduce the invention must treat it like a sign. He must ensure the meanings are as stated in the disclosure. An expert witness in a lawsuit must also treat the invention as a sign. He must determine infringement based on whether the meanings recited in the claim are present.
This patent clearly recites some semantical relationships. People who implement an anti-lock brake system relying on the same computation may infringe on the patent. There is an issue of whether the advancements over the prior art is in the physical device or in a human understanding of an obvious combination of old physical elements. The first step is passed and we proceed to the next step.
The difference between the scenarios is what the patentee regards as his invention. If he believes it is an application of the laws of physics he can claim his invention in physical terms. But if he thinks the invention is about semantics he can claim it that way too. The test will be passed or not passed depending on how the claim is written. People are free to claim an anti-lock brake system which operates entirely according to the laws of physics and leave the interpretants out of the patent. And they are free to claim an invention involving an interpretant if they believe there is an element in the claim that distinguish it from an abstract idea.
Please note how the first step correctly separates patent claims which involve some semantical relationships from claims entirely relying on causal relationships. It distinguishes patent claims which involve signs from claims which don't.
Identifying Claims on the Referent
Assuming the claim passes the first step, the second step is to identify whether the claim as a whole is written to the sign or whether the sign is merely an element of the invention. In the latter case there must be at least one significant non-symbolic element. I use the word 'significant' because the analysis must comply with the requirements the Supreme Court has set forth in Flook and Mayo.
This second step too is a threshold step. If the claim contains at least one such element it is not written to a manipulation of symbols and the sign doctrine doesn't apply. Otherwise we move to the third and final step.
I think a semiotic framework allows to define precisely what 'significant' means. The non-symbolic elements are significant when the utility of the claim as a whole is substantially different from the utility of the sign taken alone. This is a recognition that signs may be useful. There are people who argue that claims on abstract ideas cannot be useful. I reject this view because claims on signs can both be useful and run afoul of the sign doctrine.
The analysis goes as follows. First we identify in the claim those elements which constitutes the sign. Then we identify what is their purpose, their 'utility' in patent-speak. Then we identify the utility of the claim when taken as a whole. If the two utilities are substantially different the non symbolic elements are significant and the claim is not written to a manipulation of symbols. Otherwise the claim as a whole does nothing more than the manipulation of symbols taken alone and the sign doctrine should be applied.
In the anti-lock brake system the sign element is the programmed microprocessor. Its utility is to inform us of how the brakes should be activated. This information is presented in the form of a series of numeric values representing the pressure which should be applied to the brakes at any given time.
The utility of the claim as a whole varies depending on which non-symbolic elements are recited. In one scenario the claim recites an element of actually applying the pressure on the brake. Then the utility of the claim is to actually brake the car in a non-blocking manner. This is substantially different from merely informing us of how to activate the brakes. This element is significant. The claim as a whole is not written to a sign and the sign doctrine does not apply.
In another scenario the claim doesn't include the element of actually braking the car. Many other non-symbolic elements may be added. There could be a mention of the sensors attached to the wheels and the wheels themselves. The sensors attached the gas pedal and the brake pedal may be recited. The claim may go as far as mentioning the car, the driver and the slippery road. But even when all these elements are included the utility of the claim as a whole is still to inform us of how the brake should be activated. The two utilities are not substantially different. The non-symbolic elements are not significant. The claim as a whole is written to a sign and the sign doctrine is applicable.
Please note how the difference between the two scenarios is related to the referent. In the first scenario the claim actually does what the sign means. This is the referent. In the other scenario this referent is only referenced as the meaning of the sign, it is not a physical element of the invention. This distinction is crucial. When the referent is not actually part of the claim a mere reference to it is an interpretant. But when the referent is actually present the invention is more than a mere thought in the human mind. An actual embodiment of the idea is claimed. This will show up in the test as a substantial difference in utility.
We see the same thing in the famous claim in Diamond v. Diehr. It includes the step of actually curing the rubber. The utility of the sign part of this claim is to let us know how long to cure the rubber. The utility of the claim as a whole is to actually cure the rubber. The referent is included. Omit the referent and this is only a claim on the abstract mathematical computation.
Collins explains that the Federal Circuit routinely ignores this distinction:19
[T]he semiotic framework suggests that the Federal Circuit should reconsider the routine patentability of newly invented computer models. When addressing computer models, the Federal Circuit today elides the sign-vehicle with the sign and therefore commits a classic semiotic error: it inappropriately reifies a newly invented semiotic meaning into a new intrinsic property of a tangible, extra-mental artifact. As a result, it sanctions a patent on a meaningful thing even when the only invention at issue resides in the mind of the person who understands the thing's newly invented semiotic meaning. Claims to newly invented computer models literally describe a programmed computer (a sign-vehicle), yet the only inventive aspect of the claimed technology may be a new mental state in the mind of a computer user (an interpretant).
This is the very point captured by the calculator experiment. Type in 12+26 on a pocket calculator. The result is 38. Now assume you add apples and type in 12 apples + 26 apples. The result is 38 apples. Do you see a difference in the calculator? Collins says the Federal Circuit grants patents on software based on the grounds that when this kind of semantics is given to a computer data they think a new machine is invented.
Identifying claims on Newly Engineered Physical Sign-Vehicles
Once a claim passes the first two steps and it is found that the sign doctrine is applicable there is one last step to be taken care of. Newly engineered physical sign-vehicles are considered patentable and I see no reason to consider them abstract. But this type of invention is not always distinguished from interpretants by the first two steps.
Consider for example a new method for encoding bits on a hard disk platter. This is a new technology for making hard disks. This invention should not be disqualified because bits may have meanings.
Let's consider a more tricky example, the Morse code.20 This is a system for representing letters and numerals using tones, lights or clicks. It is written as physical marks shaped in the form of series of dots and lines separated by spaces. At the time of Samuel Morse this was a newly engineered sign-vehicle. A correct result of the test would be to allow a patent claim on Morse code which is limited to the physical representation of the symbols without claiming the actual text. On the other hand the test should bar a patent on Morse code which would have the effect of patenting the text.
Interpretants and newly engineered sign-vehicles may be distinguished using Collins' proposed sign doctrine. The claim is written to a patent ineligible abstract idea when the only nonobvious improvements over the prior art are interpretants. Collins mentions that the sign doctrine requires the use of a patentable-weight approach as opposed to a sign-as-a-whole approach. Interpretants should be given no patentable weight in the sense that they are not allowed to distinguish the claim over the prior art. But if something which is not an interpretant distinguishes the claim over the prior art then the patent may be granted.
A patentable-weight approach would give the correct result on a Morse code patent. Physical representations of letters and numerals are not ideas in the mind of human beings. They are sign-vehicles. A claim on a system to represent letters and numeral according to Morse code would be granted because at the time of Samuel Morse this particular sign-vehicle was a new and nonobvious advance over the prior art. It is suitable for use in telegraphic applications. On the other hand the text so represented is an interpretant. A claim directed to text written in Morse code would be rejected if the only nonobvious advancement is the encoded text.
The result of applying a patentable-weight approach to the anti-lock brake system depends on what exactly is being claimed.
In one scenario the claim may recite some new and nonobvious element of hardware. May be the sensors which measure the rotation of the wheel are an innovation. Or the microprocessor may use some new element of circuitry which is especially good at computing the anti-locking algorithm. These elements are not interpretants. They would be allowed to distinguish the invention over the prior art and the claim would be patent eligible. This is the correct result. People are free to implement the same computation when using different hardware while the inventor of the new hardware is granted his patent.
In another scenario the only new and nonobvious elements are the algorithm and the non-mathematical meanings given to the data. These elements are interpretants. They are not given any patentable weight and the claim will not be patent eligible. Again this is the correct result. The invention is thoughts in the human mind. It is abstract ideas.
Conclusion
Semiotics define concepts and vocabulary that let us state precisely what makes an abstract idea in a software patent abstract. When the only advance over the prior art is the syntax and semantics of the bits accompanied with the operations of arithmetic and logic, then the invention is an interpretant. It is a thought in the mind of programmers. This circumstance may be identified with a three step test limited to signs. It will not bar patent claims on inventions which are not signs. And it will bar patent claims on signs only when there is no invention outside of advancements in human understanding.
The doctrine that programming a computer makes a new machine conflates interpretants with physical improvements to computers. It should be abandoned.
Reference
[Collins 2010] Collins, Kevin Emerson, Semiotics 101: Taking the Printed Matter Doctrine Seriously ,
Indiana Law Journal, Vol 85, pp.1379-1443 (2010) (PDF). In this article, I assumed Professor Collins' explanation of semiotics 101 and his legal analysis of the printed matter doctrine are correct.
Footnotes
1 The exact complaint is: (emphasis in the original)
The abstractness of the "abstract ideas" test to patent eligibility has become a serious problem, leading to great uncertainty and to the devaluing of inventions of practical utility and economic potential. See Donald S. Chisum, Weeds and Seeds in the Supreme Court's Business Method Patent Decision: New Directions for Regulating Patent Scope, 15 Lewis & Clark L. Rev. 11, 14 (2011) ("Because of the vagueness of the concepts of an `idea' and `abstract,'… the Section 101 abstract idea preemption inquiry can lead to subjectively-derived, arbitrary and unpredictable results. This uncertainty does substantial harm to the effective operation of the patent system."). In Bilski, the Supreme Court offered some guidance by observing that "[a] principle, in the abstract, is a fundamental truth; an original cause; a motive; these cannot be patented, as no one can claim in either of them an exclusive right." Bilski II, 130 S. Ct. at 3230 (quoting Le Roy v. Tatham, 55 U.S. (14 How.) 156, 175 (1852)). This court has also attempted to define "abstract ideas," explaining that "abstract ideas constitute disembodied concepts or truths which are not `useful' from a practical standpoint standing alone, i.e., they are not `useful' until reduced to some practical application." Alappat, 33 F.3d at 1542 n.18 (Fed. Cir. 1994). More recently, this court explained that the "disqualifying characteristic" of abstractness must exhibit itself "manifestly" "to override the broad statutory categories of patent eligible subject matter." Research Corp., 627 F.3d at 868. Notwithstanding these well-intentioned efforts and the great volume of pages in the Federal Reporters treating the abstract ideas exception, the dividing line between inventions that are directed to patent ineligible abstract ideas and those that are not remains elusive. "Put simply, the problem is that no one understands what makes an idea `abstract.'" Mark A. Lemley et al., Life After Bilski, 63 Stan. L. Rev. 1315, 1316 (2011).
2 Please note what is NOT said. A program is not a mathematical formula. It is not argued software is mathematics because it could be described mathematically. There are people who believe the sentence "software is mathematics" means one or the other of the statements. This is incorrect and not the argument.
3 See the abstract of Collins article.
4 See [Collins 2010] pp. 1408-1411 (pp. 30-33 in the PDF)
5 See [Collins 2010] p. 1415 (p. 37 in the PDF). Also please note that this quote reflects Collins' view that a sign-vehicle is always a physical thing. I disagree. Intangible entities like mathematical symbols and numbers may also be sign-vehicles because they may have meanings defined by conventions. See part 1 of this series of article for the difference between a mathematical symbol and its physical representation,
6 This is assuming the computer uses DRAM technology for main memory.
7 Please note that the instructions by themselves do nothing. They are like travel directions written on paper. They don't drive the car. The driver does. The charges in main memory are just bits of data. The CPU is the active component doing the work. I feel the need to mention this because Collins quotes Pamela Samuelson thus: (See [Collins 2010] footnote 229 pp. 1421-1422, pp. 43-44 in the PDF)
There is one very simple but important difference between a book which contains a set of instructions about how to do a particular task and a computer program in machine-readable form which contains a similar, if considerably more elaborate, set of instructions on the same subject: The former informs a human being about how the task might be done; the latter does the task.
Programs don't do the task. Also programs in executable form are readable to programmers using disassemblers. This distinction doesn't match reality.
8 See [Collins 2010] p. 1422 (p. 44 in the PDF)
9 Collins discusses when a patent claim on a sign-vehicle may be granted. See [Collins 2010] p. 1424 (p 46 in the PDF). (emphasis added, footnotes omitted, )
Construed in semiotic terms, the printed matter doctrine states that a claim to a sign-vehicle is not eligible for patent protection if the sole locus of the improvement over the prior art resides in the interpretant that it signifies to an interpreter. The negative corollary of this limited rule is that there are many situations in which newly engineered sign-vehicles are eligible for patent protection.
For example, as already discussed, the negative corollary leads to the conclusion that newly engineered sign-vehicles are patent eligible when they have been engineered to possess non-semiotic properties in addition to their semiotic properties. Sometimes, the non-semiotic properties are structural properties of the sign-vehicle itself. A sheet of paper with a specific diagram printed on it is a sign-vehicle that is eligible for patent protection if the chemical composition of the ink in which the diagram is printed is a nonobvious invention. Sometimes, the nonsemiotic properties are the structural properties of the sign-vehicle that deterministically cause reactions in other systems. Newly engineered signals and stimuli are usually patent eligible for this reason despite the fact that they are frequently sign-vehicles as well. In either case, the advance over the prior art resides in a property other than the ability of the sign-vehicle to signify interpretants and, indirectly, refer to referents.
The structural- and functional-relation cases, which are traditionally viewed as exceptions to the printed matter doctrine, populate another category of newly engineered sign-vehicles that are eligible for patent protection under the negative corollary. Sign-vehicles have historically been patentable under the printed matter doctrine when they have been engineered so as to improve the efficiency of the process of signification without an accompanying improvement in what is signified.
Please note the criteria in bold. In software we have the opposite situation. A computer program is an improvement of what is signified without an electrical level improvement of the machine.
10 There are circumstances where the internal state of a computer used by the end-user will be inspected by a programmer. For example if a program crashes because of a bug, a memory dump may be taken and its contents may be inspected for debugging purposes.
11 I am insisting heavily on this point because lawyers often seem to assume that what is not visible to the end-user is not a sign. In particular, Collins makes this mistake. See [Collins 2010] p. 1421 (p. 43 in the PDF)
The binary ones and zeros recorded on an old-fashioned computer punch card or a newfangled USB drive are signals or stimuli: the mechanical or electronic devices into which they are fed are interpreters that, when functioning properly, produce responses through deterministic processes. No interpretants are required for software recorded on a disk to "mean" something in the nonsemiotic sense to a computer as an interpreter.
12 Video on a DVD is normally compressed to save space. This format cannot be directly displayed on a screen. The video must first be decompressed.
13
Here is an extract of judge
Newman's
concurrent opinion. Judge Rader's concurrent opinion on the same case contains a similar error. For the purposes of this article it suffices to quote Judge Newman:
Alappat's rasterizer is an electronic device for displaying a smooth waveform by selective illumination of pixels. The Alappat rasterizer operates by performing a sequence of steps in accordance with instructions that are generated electronically. This operation requires several mathematical calculations that are performed with the aid of microelectronic circuitry, and can be performed by a digital computer. The structure resides in the configuration by which the device operates, as Judge Rich has explained, and is independent of how that configuration is provided. The structure may reside in semiconductor chips and hardwired connections, or be permanently embedded in the electronic form designated read-only memory, or removably embedded in the electronic form designated random-access memory. It is not relevant to section 101 whether the structure is hard-wired or programmed, machine-readable or manually performed, and indeed the means-plus-function style of claim accommodates these alternatives.
Devices that work by way of digital electronics are not excluded from the patent system simply because their mechanism of operation can be represented by mathematical formulae. The output of an electronic device or circuit may be approximated to any required degree as a mathematical function of its current state and its inputs; some devices, such as the transistor, embody remarkably elementary mathematical functions. Principles of mathematics, like principles of chemistry, are "basic tools of scientific and technological work". Benson, 409 U.S. at 67, 93 S.Ct. at 255. Such principles are indeed the subject matter of pure science. But they are also the subject matter of applied technology.
Digital electronic devices implement mathematical manipulations of electronic signals, as chemical structures and reactions implement principles of molecular behavior. An apparatus that is configured to perform specific electronic procedures in accordance with instructions that require numerical measurements and mathematical calculations is no less statutory than any other combination of steps and components.
This view doesn't contain any notion of semantics or semiotics. Sign-vehicle, interpretant and referent are conflated. The judge considers the invention to be solely the physical device. She pays no attention to the semantical relationships.
14 See also the amicus brief (PDF) Microsoft, Phillips and Symantec submitted to the Supreme Court in Bilski vs Kappos. It contains an elaborate story of fictional computer science which concludes with these words:
Purporting to analyze the patent-eligibility of software, as opposed to that of hardware, relies on an illusory distinction. The functionality of any digital device is the product of the same transistor activity, and it is the configuration of the pathways between those transistors that dictates their functionality.
But the distinction is not illusory. The functionality of a computation is determined by the semantics of the symbols. This is not the product of transistor activity. If you examine the brief you will find that the "explanation" doesn't mention semantics. It doesn't mention bits and symbols.
This brief contains a technical error. It is apparent in this quote:
The fantastic variety in which computers are now found can obscure the remarkable fact that every single one is, at its heart, a collection of tiny on-off switches -- usually in the form of transistors. See generally David A. Patterson & John L. Hennessy, Computer Organization and Design (4th ed. 2009); Ron White, How Computers Work (8th ed. 2005). Just as the configuration of gears and shafts determined the functionality of Babbage's computers, it is the careful configuration of these on-off switches that produces the complex and varied functionality of modern computers.
Today, these on-off switches are usually found in pre-designed packages of transistors commonly known as "chips." Thin wafers of silicon, chips can contain many millions of transistors, connected to one another by conductive materials etched onto the chip like a web of telephone lines. They are organized such that they can be turned on or off in patterned fashion, and by this method, perform simple operations, such as turning on every transistor whose corresponding transistor is off in the neighboring group. From these building blocks, mathematical and logical operations are carried out. Patterson & Hennessy, supra, at 44-47 & App. C.
The challenge for the inventor is how to use these transistors (and applying the principles of logic, physics, electromagnetism, photonics, etc.) in a way that produces the desired functionality in a useful manner. Computer programming is an exercise in reductionism, as every feature, decision, and analysis must be broken down to the level of the rudimentary operations captured by transistors turning on and off. This reductionism is matched by the detail with which transistors must be configured and instructed to carry out the thousands or millions of operations required by the process.
ENIAC -- the first general-purpose electronic digital computer, functioning at the midpoint of the Twentieth Century -- could take days to program, with operators physically manipulating the switches and cables. Patterson & Hennessy, supra, at 1.10.
Fortunately, this is no longer the case. Transistors, packaged onto silicon chips, permit electronic manipulation of the pathways between them, allowing those pathways to be altered to implement different processes without direct physical manipulation. The instructions for this electronic reconfiguration are typically expressed in computer software.
A picture is worth a thousand words. You may see here a picture of how the early ENIAC was programmed. It shows the plug board where wires were manually connected. An ENIAC programmer had to pull out the wires from the old program and insert different wires for the new program. This operation actually configured a new circuit.
You may compare the ENIAC with this picture of a modern integrated circuit viewed through a microscope. Another similar picture is here. The ribbon-like structures are the pathways between transistors mentioned in the brief. Where are the transistors? They are not visible on these pictures but their locations may be identified. Pathways may intersect. Intersections are visible on the pictures. The pathways are superimposed one on top of the other at the points of intersection. The transistors are located where the intersecting pathways are in contact. As you can see, pathways on an integrated circuit can't be disconnected and reconnected like an ENIAC plugboard. They are permanently laid out on the chip surface.
When discussing the configuration of pathways between transistors the brief is incorrectly conflating two different notions of technology. The first one is the electric conductors between the electronic components. The other is whether or not current actually flows in the conductors. These two notions serve two different purposes. The physical configuration of the conductors connects components together. It creates the pathways where the current may flow. But transistors are devices which apply voltages to a conductor. If the voltage is zero, no current flows and this is usually interpreted as the bit 0. If the voltage is not zero the current flows and this is usually interpreted as the bit 1. In both scenarios a bit of data is represented by the voltage. The function of connecting components together is not the same thing as representing a bit of data.
The brief gives the impression that modern computers are programmed by reconfiguring the electrical conductors like an early ENIAC. But an integrated circuit doesn't allow to reconfigure the conductors, Modern computers are programmed by giving a program as input to the instruction cycle. This is another concept which isn't mentioned in the brief but must be present in a technically correct explanation.
The brief gives the impression that transistor activity is equivalent to the configuration of conductors. Transistors don't do that. Transistors control the voltages which are used to represent bits. The activity of the transistors is the manipulation of the bits.
But the fundamental problem with the brief is not the technical error. It is that it misrepresents the nature of the invention in software. It makes believe that the distinction between a software patent and a hardware patent is illusory. They achieve this result by never using any word which may indicate the presence of symbols and their semantics. An unwary reader may never notice that a complete and accurate explanation of software requires these notions.
15 Judge Rich wrote a dissenting opinion in In re Johnston (September 19, 1974) (emphasis in the original):
I am quite familiar with the legal doctrine that a new program makes an old general purpose digital computer into a new and different machine. This court has been through that many times and I am not denying the validity of this principle -- which partakes of the nature of a legal fiction when it comes to drafting claims. My problem is that, knowing the
invention
to be a new program, I must decide whether it is patentable in any claimed form in view of
Benson,
whether claimed as a machine, a "machine system," or otherwise.
16 See [Collins 2010] p. 1419 (p. 41 in the PDF)
17 See [Collins 2010] p. 1421 (p. 43 in the PDF)
18 See [Collins 2010] p. 1430 (p 52 in the PDF)
19 See [Collins 2010] p. 1443 (p 65 in the PDF)
20 Collins reports that the Morse code has been patented and the claim has been upheld by the Supreme Court in O'Reilly vs Morse. See [Collins 2010] footnote 251 p. 1426 (p 48 in the PDF)
|
|
|
|
| Authored by: tiger99 on Thursday, November 29 2012 @ 08:01 AM EST |
| If needed. [ Reply to This | # ]
|
- algorithm the instruction -> algorithm is the instruction - Authored by: Anonymous on Thursday, November 29 2012 @ 08:52 AM EST
- 1 lawyer + 1 lawyer = 2 lawyers should read 1 lawyer + 1 lawyer = 2 many :-) - Authored by: Anonymous on Thursday, November 29 2012 @ 09:39 AM EST
- Corrections here please - Authored by: Anonymous on Thursday, November 29 2012 @ 10:16 AM EST
- (multiple corrections) - Authored by: stegu on Thursday, November 29 2012 @ 12:35 PM EST
- Programming a computer requires to define the data. --> ? - Authored by: Anonymous on Thursday, November 29 2012 @ 12:55 PM EST
- Hands, not handles - Authored by: songmaster on Thursday, November 29 2012 @ 01:34 PM EST
- Please correct footnote 2 -- a program is a mathematical formula - Authored by: Anonymous on Thursday, November 29 2012 @ 02:00 PM EST
- Multiples correctionses - Authored by: Imaginos1892 on Thursday, November 29 2012 @ 02:04 PM EST
- Infinitive verbs vs gerunds - Authored by: Gringo_ on Thursday, November 29 2012 @ 02:20 PM EST
- they aren't [a] count of apples - Authored by: Anonymous on Thursday, November 29 2012 @ 07:29 PM EST
- found found -> found - Authored by: Anonymous on Thursday, November 29 2012 @ 07:40 PM EST
- concurrent => concurring? - Authored by: Anonymous on Friday, November 30 2012 @ 09:51 AM EST
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 08:01 AM EST |
| Let Daryl know Groklaw is still
around Or mog lol. [ Reply to This | # ]
|
| |
| Authored by: tiger99 on Thursday, November 29 2012 @ 08:02 AM EST |
| We will devise a suitable punishment for anyone who posts on-topic stuff here! [ Reply to This | # ]
|
- Six Provo office buildings sold to East Bay Technology Park - Authored by: Anonymous on Thursday, November 29 2012 @ 11:29 AM EST
- Off topic here please - Authored by: red floyd on Thursday, November 29 2012 @ 03:17 PM EST
- 3D Systems suing Formlabs - Authored by: Anonymous on Thursday, November 29 2012 @ 06:08 PM EST
- Weev Lives - Authored by: Anonymous on Thursday, November 29 2012 @ 07:55 PM EST
- Flexible rectangles with rounded corners! - Authored by: tiger99 on Friday, November 30 2012 @ 04:47 AM EST
- Evolution Teaching - Authored by: Anonymous on Friday, November 30 2012 @ 04:53 AM EST
- Was Darl onto something ? - Authored by: Anonymous on Friday, November 30 2012 @ 04:57 AM EST
- Microsoft's Common Public License - Authored by: odysseus on Friday, November 30 2012 @ 06:07 AM EST
- Dept. of Justice, FTC to Hold Workshop on Patent Assertion Entities - Authored by: Anonymous on Friday, November 30 2012 @ 06:51 AM EST
- Whorer King Coins Half Counterfeit - Authored by: Anonymous on Friday, November 30 2012 @ 11:08 AM EST
- The Push for Patents - Authored by: artp on Friday, November 30 2012 @ 02:05 PM EST
- So you took a Screenshot... - Authored by: Anonymous on Friday, November 30 2012 @ 03:29 PM EST
- The Hard Numbers - Authored by: Anonymous on Friday, November 30 2012 @ 05:54 PM EST
- Facebook: 'social network of the past' - Authored by: Anonymous on Friday, November 30 2012 @ 06:30 PM EST
- Raspberry not everybody's taste of Pi - Authored by: Anonymous on Friday, November 30 2012 @ 09:50 PM EST
| |
| Authored by: tiger99 on Thursday, November 29 2012 @ 08:05 AM EST |
Comments on the Groklaw Newspicks should go here. Please make a link so the item
is still accessible once it scrolls down off the page.[ Reply to This | # ]
|
- Facebook makes it official: You have no say - Authored by: Anonymous on Thursday, November 29 2012 @ 02:41 PM EST
- Is the pending German Copyright Bill good or bad for the Web? - Authored by: Anonymous on Thursday, November 29 2012 @ 03:30 PM EST
- PJ I thought you were boycotting AP issuances - Authored by: Anonymous on Thursday, November 29 2012 @ 04:35 PM EST
- Linux arrives on loaded Dell ultrabook - Dell still gets it wrong - Authored by: Anonymous on Thursday, November 29 2012 @ 05:00 PM EST
- Sputnik – Dell’s Ubuntu-based developer laptop is here - Authored by: Anonymous on Thursday, November 29 2012 @ 05:12 PM EST
- Do these Dell/Ubuntu ultrabooks have UEFI ? (n/t) - Authored by: Anonymous on Thursday, November 29 2012 @ 06:03 PM EST
- No customization - Authored by: kg on Thursday, November 29 2012 @ 07:06 PM EST
- Linux arrives on loaded Dell ultrabook - Dell still gets it wrong - Authored by: stegu on Thursday, November 29 2012 @ 07:12 PM EST
- Is the inability to find on website... - Authored by: say_what on Thursday, November 29 2012 @ 07:54 PM EST
- Dell Linux: Well hidden, overpriced, poor choices - Authored by: Anonymous on Friday, November 30 2012 @ 12:53 AM EST
- system76 - Authored by: Anonymous on Friday, November 30 2012 @ 01:17 PM EST
- Dell statement is lying... - Authored by: Anonymous on Friday, November 30 2012 @ 04:25 AM EST
- Linux arrives on loaded Dell ultrabook - Dell still gets it wrong - Authored by: Anonymous on Friday, November 30 2012 @ 10:20 AM EST
- Oracle drops all patents from appeal against verdict in google case - Authored by: Anonymous on Friday, November 30 2012 @ 03:04 AM EST
- How a fake Google news story spread online - Authored by: JamesK on Friday, November 30 2012 @ 07:50 AM EST
- Nokia suing Android device makers over patent on sorting text messages - Authored by: Anonymous on Friday, November 30 2012 @ 10:23 AM EST
| |
| Authored by: tiger99 on Thursday, November 29 2012 @ 08:06 AM EST |
| Transcripts of the Comes documents, that is. [ Reply to This | # ]
|
| |
| Authored by: tiger99 on Thursday, November 29 2012 @ 08:07 AM EST |
| See previous article for what this is about, and please do cast your vote! [ Reply to This | # ]
|
| |
| Authored by: chriseyre2000 on Thursday, November 29 2012 @ 08:11 AM EST |
In order to properly make the argument that software is mathematics you need to
start by explaining to lawyers what mathematics is. There is far more to this
subject than simple arithmatic. Mathematics is formal reasoning about abstract
patterns.
This will make arguments that software is mathematics much easier.[ Reply to This | # ]
|
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 09:06 AM EST |
Even a three year old child knows that software is not mathematics. Show her a
iPhone without a game and an iPhone with a game. She will pick the one with a
game because she will have much more fun with the second device than the first.
She will probably even call it "mine."
Although no government in any country on earth agrees with you, it is legitimate
to believe that patents are bad. However, there really is nothing special about
software patents that distinguishes them over other type of patents. There are
regularly patent lawsuits in all technology areas. Litigation is almost always
reserved for the worst patents, because the parties typically settle if the
asserted patent is a strong one.
Your assumption that the lawyers do not understand computers is incorrect. Many
of the patent attorneys involved in patent litigation involving software have
advanced degrees and extensive industry experience in software. What is lacking
on this blog is an understanding of the legal and business worlds.
Contrary to the apparent assertions in this blog, software patents cannot be
infringed by merely performing steps in one's mind. Under current law, any
method claim that can be infringed by performing all of the steps of the claim
in a person's head is invalid. [ Reply to This | # ]
|
- Please don't feed the trolls. - Authored by: celtic_hackr on Thursday, November 29 2012 @ 09:29 AM EST
- What Does "Software Is Mathematics" Mean? Part 2: A Semiotics Approach to the Patent Eligibility of Software by PolR - Authored by: Anonymous on Thursday, November 29 2012 @ 09:33 AM EST
- What Does "Software Is Mathematics" Mean? Part 2: A Semiotics Approach to the Patent Eligibility of Software by PolR - Authored by: designerfx on Thursday, November 29 2012 @ 09:36 AM EST
- What Does "Software Is Mathematics" Mean? Part 2: A Semiotics Approach to the Patent Eligibility of Software by PolR - Authored by: PolR on Thursday, November 29 2012 @ 10:13 AM EST
- What Does "Software Is Mathematics" Mean? Part 2: A Semiotics Approach to the Patent Eligibility of Software by PolR - Authored by: Anonymous on Thursday, November 29 2012 @ 10:57 AM EST
- What Does "Software Is Mathematics" Mean? Part 2: A Semiotics Approach to the Patent Eligibility of Software by PolR - Authored by: Anonymous on Thursday, November 29 2012 @ 12:03 PM EST
- Software is an Idea - Authored by: Anonymous on Thursday, November 29 2012 @ 12:14 PM EST
- To parent poster - Authored by: Anonymous on Thursday, November 29 2012 @ 12:24 PM EST
- A three-year-old doesn't know what mathematics is. - Authored by: Anonymous on Thursday, November 29 2012 @ 02:01 PM EST
- The troll has been well fed! -- n/t - Authored by: Gringo_ on Thursday, November 29 2012 @ 02:30 PM EST
- Really great troll! - Authored by: Anonymous on Thursday, November 29 2012 @ 02:36 PM EST
- Tortured Logic - Authored by: Anonymous on Friday, November 30 2012 @ 05:32 PM EST
- What Does "Software Is Mathematics" Mean? Part 2: A Semiotics Approach to the Patent Eligibility of Software by PolR - Authored by: Anonymous on Sunday, December 02 2012 @ 08:09 PM EST
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 09:45 AM EST |
I read this (with great difficulty) and this from someone
who obtained a physics degree and has been in the IT field
as a programmer, and system admin for over 20 years.
However, as I read it, I think I achieved my own "epiphany"
regarding software patents. And that is, software patents
don't meet the contract of disseminating the knowledge of
"how to" do something.
Look at virtually any software patent (let's take
bounceback).
It describes "what happens" (a finger drags a UI element to
a border, and it bounces back).
It doesn't tell me as "one reasonably knowledgeable of the
art" how to do it. How do I write the code to make that
happen?
I always thought patents were about the "how" not the
"what".
-Paul
[ Reply to This | # ]
|
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 09:52 AM EST |
> What Does "Software Is Mathematics" Mean?
Not much, if anything. It would not be the first area of an otherwise
"unrestricted" area that legislators have carved out and made non-free
(e.g. free-speech/crowded-theater). It is frustrating that so much energy is
wasted on this kind of hair splitting on groklaw, when there are real problems
with software patents.[ Reply to This | # ]
|
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 11:03 AM EST |
Not done reading yet, but i got to this part:
For a programmer, an
unattended computer is like a book sitting on a shelf. This book isn't currently
read but its meaning is available to whoever opens it. Similarly, no one checks
the internal state of a programmed computer once the program is done debugging.
But programmers know that if they inspect it they will read the meanings.10
The implication is that the internal activity of a computer is a sign
even when it is not actually examined by a live human. This is the correct
result. According to semiotics, a device is a sign whenever there is some
convention on how to interpret its meaning. The requirement is not that someone
actually applies the convention. It is that the convention must be defined. Then
if someone comes along and uses the convention, the meaning could be understood.
Couldn't it be reasonably argued that production code has
removed the debugging capabilities, therefore even a programmer can't "open the
book and read it"? Thus the internal activity of a computer is not a sign
because there is no convention on how to interpret its meaning.
Just
food for thought. I like the read so far though. Thanks.
~ukjaybrat -
IANAL[ Reply to This | # ]
|
| |
| Authored by: dio gratia on Thursday, November 29 2012 @ 12:10 PM EST |
A Theory of Computer Semiotics by Peter Bøgh
Andersen. My kid sister was kind enough to send me a copy for my last birthday,
although she paid less that what Amazon is currently asking.
There's a review of the book at
UPenn (PDF). The author has an abstract of the second edition that can be found
here. It's part of the Cambridge Series on Human-Computer Interaction, and I
believe you can get paid access to an Adobe ebook version through Cambridge Books Online.
[ Reply to This | # ]
|
| |
| Authored by: Ian Al on Thursday, November 29 2012 @ 12:17 PM EST |
The Supremes said that the Bilski patent was a patent on abstract ideas, but I
have always been uncomfortable because the approach they took was to look for
evidence of non-abstract ideas and come to their conclusion on that
basis.
The concept of hedging, described in claim 1 and reduced to
a mathematical formula in claim 4, is an unpatentable abstract idea, just like
the algorithms at issue in Benson and Flook . Allowing petitioners to patent
risk hedging would pre-empt use of this approach in all fields, and would
effectively grant a monopoly over an abstract idea.
Petitioners’ remaining claims are broad examples of how hedging can be used in
commodities and energy markets. Flook established that limiting an abstract
idea to one field of use or adding token postsolution components did not make
the concept patentable.
That is exactly what the remaining claims in
petitioners’ application do. These claims attempt to patent the use of the
abstract idea of hedging risk in the energy market and then instruct the use of
well-known random analysis techniques to help establish some of the inputs into
the equation.
Indeed, these claims add even less to the underlying
abstract principle than the invention in Flook did, for the Flook invention
was at least directed to the narrower domain of signaling dangers in operating a
catalytic converter.
There seems to be nothing in that explanation
that indicated what sort of hedging method invention would not be an abstract
idea. If the process actually made the investments and counted the profits,
would that transform it into non-abstract, patentable subject matter?
I
have, of recent days, been saying that patenting functions documented in patent
claims was patenting abstract ideas. I have had my fingers crossed in case
someone thought to challenge that assertion. The abstract ideas used in writing
software have a non-abstract conclusion since they end in written (hopefully
working) code. However, if Bilski was abstract ideas, it shows that the ideas
can still be abstract even when the subject of those ideas, hedging, is not. I
will read your latest piece with enthusiasm in the hope that you have provided a
scientific and rigorous proof of what is abstract thought and what is
not.
I have, of recent days, been saying that patenting functions
documented in patent claims was patenting abstract ideas. I have had my fingers
crossed in case someone thought to challenge that assertion. The abstract ideas
used in writing software have a non-abstract conclusion since they end in
written (hopefully working) code. However, if Bilski was abstract ideas, it
shows that the ideas can still be abstract even when the subject of those ideas,
hedging, is not.
I will read your latest piece with enthusiasm in the
hope that you have provided a scientific and rigorous proof of what is abstract
thought and what is not.
---
Regards
Ian Al
Software Patents: It's the disclosed functions in the patent, stupid! [ Reply to This | # ]
|
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 12:27 PM EST |
Your clock analogy is not correct.
The convention for reading time
may be changed. This makes the clock a sign according to semiotics. For example,
suppose we decide to use a decimal time system. In this system there are 20
hours in a day, 10 before noon and 10 after. Each hour is divided in 100 minutes
and each minute is divided in 100 seconds. We can easily build a clock that
keeps time according to this new system. We just have to paint the numbers 1 to
10 on the old clock in place of the old numbers. Then the position of the
handles can be interpreted according to the new convention. The short handle
indicates the hour and the long handle indicates the minutes if you mentally
multiply the numbers by 10.
Here is the abstract idea question. Did we
invent a new clockwork which performs its functions according to the law of
physics? Or did we invent a new way to interpret the meaning of an old clock? Of
course, in the decimal clock example the clockwork was not changed. The
invention amounts to painting new numbers on the clock.
This is not
inventing a new clock.
Getting a clock to turn the hands to
represent half of a 20 hour / 100 minute day would require change in the gearing
of the minute hand. Simply relabeling the face does not change the fact that
that the minute hand of a 12/60 clockwork would rotate 12 times per half day,
not 10. Having said that, I don't know if a 10/100 clockwork would be
considered patentable subject material.
[ Reply to This | # ]
|
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 12:58 PM EST |
This always seemed to me to be a pointless approach. It is Congress you need to
influence, not the Supreme Court.
The Constitution grants extremely broad powers to Congress:
"Congress shall have the Power to promote the Progress of Science and
useful Arts, by securing for limited Times to Authors and Inventors the
exclusive Right to their respective Writings and Discoveries"
There is no fine nuance here regarding what kinds of inventions, etc., are
eligible. That is the matter for legislation. The Supreme Court does not
decide on policy.
If you know anything about the Supreme Court you know that they are very
hesitant to act as a legislator. They defer to the intent of Congress, and the
Executive branch, unless they have acted in contradiction of the Constitution.
That is how our government works.
But the Executive branch, through the USPTO, has repeatedly acted in support of
software patents. This has been constant policy, via both Republican and
Democratic administrations for many years. And Congress has expressed no
willingness or even interest in changing this, even though it is 100% within
their power to do so.
Expecting the Supreme Court to change fundamental policy in this area is rather
naive. [ Reply to This | # ]
|
- Then the latest copyright extensions are unconstitutional!!! - Authored by: Anonymous on Thursday, November 29 2012 @ 01:04 PM EST
- I disagree - Authored by: PolR on Thursday, November 29 2012 @ 01:07 PM EST
- I disagree - Authored by: Anonymous on Thursday, November 29 2012 @ 02:32 PM EST
- Agree - Authored by: Anonymous on Thursday, November 29 2012 @ 08:09 PM EST
- Agree - Authored by: PJ on Thursday, November 29 2012 @ 08:54 PM EST
- Agree - Authored by: Anonymous on Friday, November 30 2012 @ 04:15 PM EST
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 01:27 PM EST |
The Functions of Programmed Computers Depend on Human
Understanding
Before I start, I'm unable to create a new
account despite my announced intention to do so here as they have been
temporarily disabled.
I commend you for such a detailed and elaborate
presentation for your view point. I admit that I have not yet finished reading
let alone fully understand everything you present. My intention with this
posting is not to challenge or undermine your position in relation to software
and mathematics, but perhaps more to cause to to rethink some aspect of your
position and it's for that reason that I will do my best _not_ to engage in any
dialectic with the intention of supporting my differing viewpoint.
That
being said, I feel compelled to comment on the above blockquote.
1. "Human
Understanding" applies to the humanity in general my comments are made where
such an expression is understood to be inclusive of any human beings that have
mental capabilities within one or even two standard deviations of the
statistical norm of metal capabilities, whatever that may be. As such we
certainly can understand it _not_ to refer to individuals who are outliers of
that norm, such as mentally deficient individuals, or exceedingly brilliant or
studied individuals insofar as the requirements of understanding is not a set of
the priory stated norm.
2. "Programmed Computer" is understood to refer to
a hardware platform that holds software functionality that may or may not be
executing but only present in some part of its memory system.
3.
"Functions" is understood to refer to a some functional characteristic present
in or on a Programmed Computer whether they be machine specific or caused by
machine operations related to its execution some software. No presumption
exists that would cause a reasonable individual to believe the function is
required or executing, only that the function exists and may be executed.
So
both definitions 2 and 3 also contain no presumption that the Programmed
Computer is even turned on. In that way, it's capabilities is purely
theoretical and certainly no presumption exists that would suggest that the
Programmed Computer is performing anything useful that is not purely a result of
its tangibility.
With that, I challenge your presumption that the Functions
of a Programmed Computer depends on Human Understanding. Consider:
You
certainly don't understand the specifics of the caching functionality Google
uses, or the transaction characteristics in the filesystem they use. However
such a lack of understanding does not prevent that functionality from performing
its task(s) within the relevant "Programmed Computers" if and when conditions
may cause the the function to be performed.
Certainly the creation of the
software component that is part of the "programmed computer" requires the
understanding of one or more engineers, however that specific knowledge is not
"Human Understanding" since the engineers' specific understanding as it relates
to the making of the software component(s) is an outlier compared to normal
human mental capacities.
If your intention is to alter my definition of
"Human Understanding" to be inclusive of any and all human knowledge and mental
capacities, than you may have a valid counterargument to my challenge. But such
a homogenization of human mental capacities is a declension to a human beings
natural instinct, will and capacity to enhance his/her lives and capabilities by
acquiring new skills or assets.
Such a alteration is communistic in nature
rather than individualistic and to truly follow such a principle in an unbiased
way is to challenge the very foundation of capitalism as well as our cultural
and natural values. We may as well be trying to claim that men and woman should
not be selective about the characteristics of their friends or spouses, let
alone consider any individuals claim to intellectual property whether it be
copyright or patents. [ Reply to This | # ]
|
| |
| Authored by: OpenSourceFTW on Thursday, November 29 2012 @ 02:01 PM EST |
This article made my brain hurt, but in a good way. Thanks PoIR!
I now understand a very important point, namely, about how software does not
transform a machine.
Lets say I run Software X, which calculates the the Dow Jones average. Yes the
logic behind it may be innovative (but not patentable, it's an algorithm), but
does the execution of it significantly change the underlying computer? No, it is
still doing the same low-level operations it has always done (ADD, SUB, NEG,
etc). Nothing is inherently different. Only the meaning we attach to it is
different, and that is not enough to make it patentable.
So how can this be patentable if the machine is the same?
Another question: If someone argues that the exact number and order of these low
level operations is different for this software than for preceding software, and
that this should be patentable, then this is easy to circumvent.
Suppose the patent applicant used a particular Intel processor. What if I simply
use an AMD processor? Won't the process be somewhat different due to the
difference in hardware? Doesn't that mean I made an even newer machine? What if
I run it on my Android device? It will certainly be different there. Therefore,
the whole machine transformation argument is moot even if it was valid, because
simply changing the execution environment would produce a different machine.
The argument attempts to straddle both sides at once by claiming a specific
transformation permits the patenting of all transformations, no matter how
different, as long as they "do about the same thing." It permits the
innovation to be specific but the protection to be broad.
---
I voted for Groklaw (Legal Technology Category) in the 2012 ABA Journal Blawg
100. Did you? http://www.abajournal.com/blawg100. Voting ends Dec 21.[ Reply to This | # ]
|
- Exactly! - Authored by: Anonymous on Thursday, November 29 2012 @ 02:12 PM EST
- My "Aha" Moment - Authored by: Anonymous on Thursday, November 29 2012 @ 03:27 PM EST
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 02:31 PM EST |
The information processing functions of a computer cannot be
separated from human understanding.
100% agree.
My view is
that all information is abstract, in the same way that numbers are abstract
(i.e. they are symbols that can be manipulated mentally, not physical phenomena
that can be moved around by machines).
"Information processing" is the
manipulation of abstract symbols. Its an abstract activity: a mental, semantic
activity. We might assist it by using mechanical machines that manipulate
physical phenomena (matter or electrical charges or magnetic fields) but really
those machines just push physical stuff around, not "information". The
"information" is a semantic assocation between those physical things and
human-meaningful abstract concepts (symbols). The semantic association exists
only in the minds of the programmers and users of the machine. There is no
physical representation or embodiment of it in the machine itself. So even if
you want to do an "information processing task" with the help of the machine,
the first step (programming the machine) and the last step (interpreting the
results) require a semantic mental process to be done by a human, and the
calculations done in-between by the machine do not directly manipulate
"information" at all.
In summary:
"Information" is an abstract thing
that exists only in our minds, and "information processing" is an entirely
mental activity! (In other words, its mathematics). [ Reply to This | # ]
|
| |
| Authored by: danielpf on Thursday, November 29 2012 @ 02:34 PM EST |
To equate all software to mathematics is as reductionist as equating all
material objects to atoms.
Between writing high level code and bit flipping there are many levels of data
transformation which progressively change the meaning of what software is,
exactly as between atoms and devices there are many levels of matter
organization allowing to pass between non-patentable natural phenomenon at the
atomic level to inventions at the device level.
The high level human work may be just painting something on screen which is then
translated to a postscript program, and after some more levels to bit flipping
and finally to ink dots; it would be abusive to say that using a computer is
always software creation, so math, yet there is no sharp distinctions between
all the possible ways to create software at different levels, from assembly
language to compiled language to interpreted language to spreadsheet composition
to word processor.
Mathematicians do their best to have a precise and unique definition of the
words they use, while most other humans use language in a fuzzy way: words have
different meanings in different contexts. In between legislators try to
introduce some rigor in the laws but by far do not reach the mathematical rigor.
So in the real world the word software has a different meaning in different
contexts. I pretend that what legislators mean by software covers a different
semantic field than what computer scientists mean.
Not understanding that produces sterile discussions.
Note that I am strongly against software patents, but the software=math argument
appears to me counter-productive.
[ Reply to This | # ]
|
| |
| Authored by: sumzero on Thursday, November 29 2012 @ 03:00 PM EST |
i am inventing nothing. all i am doing is figuring out the
correct way to request from a general purpose computer
something it can already do in a way that it understands. it's
just translation work.
sum.zero
---
48. The best book on programming for the layman is "alice in wonderland"; but
that's because it's the best book on anything for the layman.
alan j perlis[ Reply to This | # ]
|
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 03:26 PM EST |
| I can't believe we went through an entire discussion of semiotics without you
using the painting "Ceci n'est pas un
pipe" ("This is not a pipe") as an illustration of the difference between
the sign carrier (the painting) and the referent (the pipe). [ Reply to This | # ]
|
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 03:35 PM EST |
This "Software is Mathematics" jabber keeps coming back to Groklaw.
Is there a point to it?[ Reply to This | # ]
|
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 03:41 PM EST |
I note in the footnote about the ENIAC a mention that no voltage is
"usually" interpreted as a logical zero. This is correct, but it
might be worth calling out a little more explicitly: the ones and zeroes are
purely convention. There is reverse logic where no voltage is a logical one and
vice versa. And we're free to choose either way when designing circuits.
So, as you say, the meaning of the voltages exists in the mind of the one using
the computer, not in the signals themselves.[ Reply to This | # ]
|
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 04:00 PM EST |
As a programmer for over 20 years, I know that programming
is math. Back in those days, computer science was often
taught by mathematicians. I would assume that any competent
professor in computing today would understand that
programming is math. So, why doesn't someone go ask the top
computer science professors whether programming is math or
not?
If I wanted to know about laws, I would ask a judge or
lawyer instead of a computer science professor. Yet when
people want to know about programming, we are asking judges
and lawyers. Makes no sense.[ Reply to This | # ]
|
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 04:55 PM EST |
This is an excellent onion gum.
It will be of exactly ZERO use to convince Senators, Representatives, Judges,
the media, lawyers, advocates, lobbyists, and decision makers of ANYTHING.
You do such a great job of making simple nuances complicated that I can't
imagine you have a career outside of academia. In the real world there's simply
no opportunity to employ anyone who takes ten words to say what could be said in
three.
Sadly it took great effort to write this, unless such obfuscatory drivel comes
naturally, and this effort will NEVER be used to effect change, improve patents,
remove software from patentability, or do more than put Groklaw readers to
sleep.
Speaking of which I didn't realize it was naptime - till I read part 2. I was
still waking up from part 1.
Anon - my job involves law and patents - clearly yours does not.[ Reply to This | # ]
|
| |
| Authored by: OpenSourceFTW on Thursday, November 29 2012 @ 06:06 PM EST |
I believe the effectiveness of an article is inversely related to the number and
vehemence of the trollish comments left.
By that criteria, this article is a success. :)
---
I voted for Groklaw (Legal Technology Category) in the 2012 ABA Journal Blawg
100. Did you? http://www.abajournal.com/blawg100. Voting ends Dec 21.[ Reply to This | # ]
|
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 06:52 PM EST |
I mentioned this on the last article, too. These essays are
enormously powerful, and if we could get our policy makers
to read them, we might have a shot at ending this plague.
I looked through the Patents section just now, and I see
there is an impressive collection of links and articles. It
is possible that PolR's work is in there somewhere. But
these essays are of such importance that I think they
deserve a dedicated section to which decision makers and
other stakeholders can be directed.
Thanks,
David Bruce[ Reply to This | # ]
|
| |
| Authored by: Anonymous on Thursday, November 29 2012 @ 07:01 PM EST |
PoIR, thank you for the thorough analysis in your continuing series. We often
have a tendency to stop right after proving to ourselves that software is a
branch of mathematics, without placing that fact in the context of an actual
patent test. I am enthusiastic about this semiotic approach that you're
describing, as a test based on the exclusion of advancements to interpretants
seems like it might be more attractive to the courts and examiners office
by-and-large than the direct proof of software being a branch of mathematics. We
know that the arguments are the same but the "Software is Mathematics"
mantra seems to be difficult for many, particularly non-programmers, to
reconcile with their own perception of software as collections of interactive
"objects" and "tools".
For the sake of completeness though, I would like to bring up one issue that may
arise from interpreting the computer as a sign when determining infringement.
You write, "The opposite view -- that there is no sign unless someone must
actually watch the sign-vehicle -- leads to absurd results." However this
is precisely how a quantum computer operates. Unlike a bit which always must
exist in one of two states, a qubit does NOT exist in any defined state until a
measurement is taken. This is not merely semantics or a lack of adequate
measuring tools, it is a fundamental principle of quantum mechanics: that qubit
does not exist in any one state until it is measured.
For the time being this is mostly an academic exercise, but we are not far away
from this becoming reality. I wonder if "quantum software" would still
be safe from patents using this test?[ Reply to This | # ]
|
| |
| Authored by: soronlin on Friday, November 30 2012 @ 06:14 AM EST |
| Old Machines
The central processor (CPU) and central
memory (CM) [of the CDC Cyber 72] operated in units of 60-bit words. In CDC
lingo, the term "byte" referred to 12-bit entities (which coincided with the
word size used by the peripheral processors). Characters were six bits,
operation codes were six bits, and central memory addresses were 18 bits.
Central processor instructions were either 15 bits or 30 bits,...
eight
18-bit address registers (A0 through A7), eight 18-bit index registers (B0
through B7), and eight 60-bit operand registers (X0 through X7). [There were no
LOAD or STORE instructions] Seven of the A registers were tied to their
corresponding X register. Setting A1 through A5 read that address and fetched it
into the corresponding X1 through X5 register. Likewise, setting register A6 or
A7 wrote the corresponding X6 or X7 register to central memory at the address
written to the A register. A0 was effectively a scratch register....
ones
complement... -- Wikipedia
The Cyber series of computers, in
common with many computers of their era, was a totally different beast than
computers of today. Whereas we have settled on word lengths that are a power of
two, two's complement arithmetic and either a register or a stack-based
approach, the Cyber series differed in all of these respects. Programming it in
assembler was a fascinating adventure.
All of which means that to implement
an invention on it, every single aspect of that implementation must necessarily
be different from the implementation on a more modern machine, even down to the
representations of the numbers, and the encoding of characters.
Toilet
Doors
On a toilet cubicle door you have a lock. This lock has a knob that
you have to move through a defined path in order to lock or unlock the door.
Except for such convoluted possibilities as RFID tags, there is no getting away
from that fact. To lock or unlock the door you have to move something in some
defined way.
That is not, in itself, patentable. It is obvious that anyone
skilled in the art of lock design could come up with several different ways to
implement such a lock:
- A simple bolt action bolt.
- A rotating knob
that uses gear teeth to move a bolt.
- A rotating knob that turns an
asymetrical plate such that in one position the plate engages the lock
plate.
- An electrical switch that powers an electromagnet.
- A pivoted bar
that rests in a bracket on the door frame in the locked position or can be
rotated 180 degrees so that it doesn't.
Each of these implementations is a
patentable invention, (excepting novelty and obviousness.)
New
Machines?
Let us now suppose that I had an implementation of a Cyber 72
on an integrated circuit, rather than a room full of equipment racks. Let us
suppose that I gave it a FORTRAN compiler. Let us suppose that I put this chip
into a mobile phone and, with malice aforethought, I implemented
slide-to-unlock. However, just to be obtuse, I made it rotate to unlock much
like invention 2 above. It still infringes the patent, but is dissimilar to the
iPhone embodiment.
One imagines that the implementation of Apple's
slide-to-unlock was written in Objective-C, or assembler. As such the bones of
their implementation is full of classes and objects, lists and collections.
FORTRAN has integers, reals and arrays, and that's all. (OK, it's got complex
numbers too.) And on the Cyber72, the integers are 60 bits, not 32 or 64, and
negative numbers are represented in one's complement rather than two's
complement. Any text is encoded in a different scheme that only has 64
characters in it rather than ASCII's 95 or Unicode's 100,000 or so.
There
would be no similarity between Apple's software and the Cyber 72 software. They
would look totally different. The APIs would be totally different. The
implementation of slide-to-unlock would therefore be totally different. If one
skilled in the art of analysing software was to compare them, the only
similarity would be at the most abstract level: "they both detect a finger
moving along a path, and they both tell the phone's OS to unlock." Possibly, but
not necessarily, they might use the same algorithm for tracking the finger
movement, but at such a high level of abstraction that one might assume that I
and Apple read the same academic paper. Algorithms as such are not
patentable.
So if programming a computer creates a new machine, then
different software must create a different machine. An infringing product
must therefore create a similar machine to any embodiment of the invention.
We have shown above that, by the rules and law, no patentable aspect of our
Cyber72 phone is similar to any aspect of the iPhone in regards to the
slide-to-unlock patent. And yet it implements every aspect of the patent
claims.
We have a situation where a product fully implements a patent in
every particular, and yet it does not infringe it. That is a paradoxical result.
In Maths, Logic and any other rigorous field, a paradox indicates that one of
your assumptions is incorrect. We have three options to escape it:
- Our
product does not infringe because the Cyber72 implementation is not the same
sort of computer with the same sort of OS and the same sort of software. But
that would significantly reduce, possibly to zero, the number of infringements
of any software patent. It would also be a minefield to determine.
- The law
is wrong. But that means that algorithms are patentable subject matter.
- The
patent is wrong, since it does not seem to describe any patentable
subject.
One might think that we could discard the notion that programming
a computer makes a new machine, but the argument still stands, albeit in more
abstract terms; we have an embodiment that shares no aspect of its constitution
with any other embodiment. The only commonality is the abstract algorithm and
the abstract concept.
I believe that everyone, even Apple, given only those
three alternatives, would choose to invalidate the patent.
It's
Mathematics, Stupid
Maths works. Every time. Consistently. It is not like
the law, which can be argued different ways on different days. On days when "is"
may be ambiguous, "=" still means the same.
Because software is mathematics,
the above argument can be applied to every patent. It will invalidate every
patent that does not have significant non-software subject matter. [ Reply to This | # ]
|
| |
| Authored by: Anonymous on Friday, November 30 2012 @ 09:56 AM EST |
Most of mathematics is equational or relational -- describing what
a formal
abstraction is in terms of simpler parts or properties,
or establishing
bounds using inequality relations.
Both mathematics and CS are complicated
by divergence. Infinite
series can be convergent (1/2 + 1/4 + 1/8 + ... = 1)
or divergent which,
in mathematics, allows "equations" that are not equal to
anything (1 + 1
+ 1 + ... = ?).
Most software abstractions are highly
divergent. You can't reason
equationally about any general purpose program
language because for a
program to be reducible to an equation requires it to be
proven halting
which cannot be done in the general case. For example, the
program
def f(i): return f(i+1)
has no answer for the
same reason as the divergent series above.
That mathematics at large is so
intolerant of divergence while
software
muddles along so well in the absence
of proofs of termination indicates
that the value of a program lies not in its
ability to define what things
are by equational thinking or to establish
bounds, but to
perform a computations that are actualized, so I think software
artifacts
are substantially different from the artifacts that result from
mathematical methods. [ Reply to This | # ]
|
| |
| Authored by: albert on Friday, November 30 2012 @ 05:49 PM EST |
and PoIR did his/her usual fine analysis, I'm afraid it's a case of pearls
before swine*. First, I'd like to see the courts definition of an abstract idea.
To me, the phrase "abstract idea" is an abstract idea! Just look up
the definitions. The phrase can have many meanings. This isn't good law. Is it
defined anywhere in a court ruling? Neither word shows up in the USPTOs document
MPEP, Appendix L. Perhaps the concept can be defined in relation to software
patents, but I think it will always be subjective. Patents are effective when
the subject is a machine. That was the original objective. You can't apply the
old law to software; it didn't exist back then. The USPTO started patenting math
circa 1976, IRRC. Now, there are at least 10 important ones (see rsa.com).
Congress should have stopped it dead then. If you can't patent math, then those
math patents are invalid.
Point #1, we already have math patents. How does this help the 'software is
math' argument? The software patent problem should not be decided in the courts,
which have been shown to be incapable of doing so. That's not a criticism of the
courts, they're just trying to apply ancient laws to modern technology. We've
seen what happens when the courts try to extend the law (Citizens United).
Sometimes, it's a disaster.
Point #2, 'IP lawyers' think software is 'intellectual property', a term with no
formal definition. Is a patent or copyright 'property'? They are treated as
property, but no, they are _protections_ of useful property, building a monetary
wall around an idea (in copyright, the _specific expression of ideas_, in
software patents, the algorithm(s) expressing the ideas). A patent is much like
a restraining order. Since patents are 'intellectual protection', we can
eliminate trolls, since they have no useful property to protect, only patents
describing the property, and universally, poor descriptions at that..
Point #3, Machines(circuits) vs. Software.
I build a really cool circuit that compresses/decompresses data in a unique way,
and patent it. I can sue anyone who copies the circuit. Now, someone comes along
with a general purpose computer that does the same algorithm in software.
Drat! I should have patented the algorithm! A circuit is a physical object.
Patent infringing is easy to detect, and deal with. What if I use gate arrays?
The programming of a gate array can be unknowable, just like a ROM program in a
CPU. How do I detect infringement? I can't, unless I can subpoena the source
code. A competitor could create a circuit that accomplished identical results,
in an entirely different manner, and escape infringement. I leave it to the
mathematicians to decide whether different algorithms can produce identical
results given the same input data, and, if so, is this a rigorous proof of
infringement.
Point #4, Algorithms vs. Processes
Some folks say that algorithms are processes, and so are patentable. They take
refuge in defining both as 'a sequence of steps that accomplish some end'. In
the old days, a process ending with a product: a chemical element, compound, or
alloy; or a physical item like a bolt, tube, rail, etc. Often, a machine wasn't
necessary. With the advent of software in everything, things got fuzzy. Let's
take the 'swipe patent', since we're sick of hearing about it. It's essentially
a patent on a gesture, or strictly, the interpretation of a gesture. How does
this bogopatent even remotely resemble a process? Does it produce a product? No,
it produces data patterns, theoretically hundreds of thousands of data patterns,
not to mention the interpretation of those patterns. Clearly, this does not
conform to the traditional concept of a product, so 'process' cannot be applied
here.
Point #5, Detection of Software Patent Infringement
How is software patent infringement detected in the marketplace? It can't be
detected, unless the situation involves a patent on an action, or series of
actions, steps, if you will (like the swipe bogopatent), playing a audio or
video file with proprietary encoding, or existing in an environment where
proprietary patents must be used (like the mobile phone), etc.
Conclusions
1. Software patents need to be eliminated. It's the simplest, fairest, and most
economical thing to do. All existing s/w patents should expire in 1 year. There
will be an explosion of innovation and competition, I guarantee.
2. Patenting algorithms needs to be eliminated, and all such patents
invalidated.
3. Process patents should produce a product, in the original sense of the word.
4. Business methods patents should be eliminated. They are even more absurd then
s/w patents (if that's possible).
Changing the law to accommodate s/w patents would be a magnitude 11 disaster.
Footnote
In my years of reading Groklaw (Thanks PJ, Mark, et.al.), I've learned a lot,
and often about things that were of no interest to me, that I now find
fascinating. Outside of this community, I still feel like a voice crying out in
the wilderness, which is frustrating sometimes. So, everyone, keep up the good
work,
I'm pullin' for ya, we're all in this together...
Albert
----------------------------------------------------------
*Caution, resist the urge to respond, look it up instead.[ Reply to This | # ]
|
| |
| Authored by: Ian Al on Saturday, December 01 2012 @ 12:50 PM EST |
I realised, early on, that PolR had missed the key aspect of applying the theory
to inventions on-a-computer. I can't believe he laid out all the facts so well
and missed this major issue!
Here is where he went
wrong:The programmer must define the conventions on the syntactic
organization of the bits and the corresponding semantics. Then he must define
the operations of arithmetic and logic which will solve the problem. This is all
interpretants.
The day some clever clogs invented assembler
language programming and soon after when more clever clogs invented higher level
languages, the programmers and computer designers were divided into many
different camps, each with their own common symbol set. There was the processor
circuit designer who shared the same sign language with the programmers who
originally coded direct to binary instructions. Assembly language programmers
had the compiler to translate the symbology defined as the assembler language
into machine code binary.
Now, as PolR points out, one can go up, layer
after layer, via a software based universal algorithm to the Dalvik assembler
level. Even then, programmers of apps do not, typically, use Dalvik assembler.
They use a higher level language such as Java because there is more in
the Dalvik virtual machine than the universal algorithm. There is also the
manipulation of objects that have Dalvik symbology and the object based
programming language must be translated into Dalvik objects (complex symbols
with properties) which are then manipulated using the Dalvik universal
algorithm.
There is also a horizontal separation which applies at each
layer of programming. It starts at the BIOS and works its way across via the
operating system, across APAs and, potentially, across further divides until it
is presented as a symbol set of library functions to the programmer. The
programmer who writes a 'Hello World' program only has access to the
print-to-screen symbols in his semiotics workspace. He knows nothing of OS
display APAs and video driver symbology.
The textual symbol, CAT, does
not refer to a specific cat, but the interpretant will usually be a small feline
suitable to be a pet (or not, if you don't like cats). Pets, feral cats and wild
cats would be referents, although this might not extend to the big cats. The
sign-vehicle in this case is the text displayed on your computer monitor.
Between the sign-vehicle I used when composing this comment and the sign-vehicle
you used when reading the sign, the symbol transferred to many other sign
vehicles.
In the good old days, one of the sign-vehicles would have
been a series of addresses containing eight-bit byte signs of ASCII code in the
guts of the computer (I'm so glad they did not patent that world standard!). I
doubt I would recognise the sign in the computer I am now using. How it looks in
an IP packet is anyone's guess.
The important thing is that I was the
author that wrote the sign. Only the interpretant is shared between us and it
exists only in our minds. The referent is sat on the mat. The sign (CAT) was
passed from sign-vehicle to sign-vehicle between us.
A high-level
language programmer does not pass the referent or the interpretant down to the
processor or out to the BIOS by the act of interpreting or compilation. In fact,
there are only signs in the source code and so there cannot be a referent or an
interpretant in the source code. The symbols specific to the program are
translated by the programmer into a mathematically valid programming language
and the interpretants of the program-specific symbols have to be described in
source code comments if they are to be shared with other programmers. Only the
interpretants of symbols in the programming language, itself, are shared between
programmers who 'know' the language (their minds contain the sign/interpretant
relationships of the computer language). The code is always just the sign part
of the triad.
Interpretants are always in the mind of the programmer
and the programmer will also have to know what the referent is in order to write
the program. The referent is what in the real world is represented by the signs
in the computer. The signs do not, typically appear to the program user. The
programmer intends the result of symbol manipulation to be 'seen' by the user
(the symbol manipulation is the sole purpose of the program).
The vital
question is which of any of this is patent protectable under patent law and is
there a test of a patent to determine if the user or installer of software
written by a writer and compiled/interpreted at several software boundaries into
machine code and installed on-a-computer can infringe on a valid
patent?
Please note that the Supreme Court has opined that no software
writing can infringe on a patent. Only the manufacture, importing, selling or
using of machines, following processes, executing methods and transforming of
materials can infringe on patents.
Lets start with Bilski because
computers are so hard. Bilski was not an on-a-computer invention. It could not
be used without a computer because of the extensive and complex mathematical
analysis and the need for extensive and timely data on energy suppliers current
deals and the institutional energy users business models. It made a buck by
estimating which energy deals could be 'sold on' to energy users, thus making a
middle man margin. The patent did not claim a computer.
The Supreme
Court found that patent law did not exclude business methods because parts of
the word of the law would have no meaning if that were the case.
The
Supreme Court found that their previous landmark cases of Benson, Flook and
Diehr showed that Bilski was insufficient to be a business method patent and
was, thus, abstract ideas.
A business method is the manipulation of
symbols. It does not matter that a symbol in the Bilski business method is of
any one energy deal any more than it is important that 'cat' means any one cat.
The Supreme Court set the principle in Bilski, Flook and Diehr that there had to
be specific and significant post-process production of a referent for a patent
to be valid. From Bilski, with all the twiddly bits removed:
Even
though petitioners’ application is not categorically outside of §101 under the
two broad and atextual approaches the Court rejects today, that does not mean it
is a “process” under §101. Petitioners seek to patent both the concept of
hedging risk and the application of that concept to energy markets. Rather than
adopting categorical rules that might have wide-ranging and unforeseen impacts,
the Court resolves this case narrowly on the basis of this Court’s decisions in
Benson , Flook , and Diehr , which show that petitioners’ claims are not
patentable processes because they are attempts to patent abstract ideas. Indeed,
all members of the Court agree that the patent application at issue here falls
outside of §101 because it claims an abstract idea.
In Benson , the
Court considered whether a patent application for an algorithm to convert
binary-coded decimal numerals into pure binary code was a “process” under §101.
The Court first explained that “ ‘[a] principle, in the abstract, is a
fundamental truth; an original cause; a motive; these cannot be patented, as no
one can claim in either of them an exclusive right.’ ” (quoting Le Roy). The
Court then held the application at issue was not a “process,” but an
unpatentable abstract idea. “It is conceded that one may not patent an idea. But
in practical effect that would be the result if the formula for
converting . . . numerals to pure binary numerals were patented in
this case.” A contrary holding “would wholly pre-empt the mathematical formula
and in practical effect would be a patent on the algorithm itself.”
In
Flook, the Court considered the next logical step after Benson . The applicant
there attempted to patent a procedure for monitoring the conditions during the
catalytic conversion process in the petrochemical and oil-refining industries.
The application’s only innovation was reliance on a mathematical algorithm.
Flook held the invention was not a patentable “process.”
The Court
conceded the invention at issue, unlike the algorithm in Benson, had been
limited so that it could still be freely used outside the petrochemical and
oil-refining industries. Nevertheless, Flook rejected “[t]he notion that
post-solution activity, no matter how conventional or obvious in itself, can
transform an unpatentable principle into a patentable process.” The Court
concluded that the process at issue there was “unpatentable under §101, not
because it contain[ed] a mathematical algorithm as one component, but because
once that algorithm [wa]s
assumed to be within the prior art, the application,
considered as a whole, contain[ed] no patentable invention.” As the Court later
explained, Flook stands for the proposition that the prohibition against
patenting abstract ideas “cannot be circumvented by attempting to limit the use
of the formula to a particular technological environment” or adding
“insignificant postsolution activity.”(Diehr).
Finally, in Diehr, the Court
established a limitation on the principles articulated in Benson and Flook .
The application in Diehr claimed a previously unknown method for “molding raw,
uncured synthetic rubber into cured precision products,” using a mathematical
formula to complete some of its several steps by way of a computer.
Diehr explained that while an abstract idea, law of nature, or
mathematical formula could not be patented, “an application of a law of nature
or mathematical formula to a known structure or process may well be deserving of
patent protection.”. Diehr emphasized the need to consider the invention as a
whole, rather than “dissect[ing] the claims into old and new elements and then …
ignor[ing] the presence of the old elements in the analysis.” Finally, the Court
concluded that because the claim was not “an attempt to patent a mathematical
formula, but rather [was] an industrial process for the molding of rubber
products, ” it fell within §101’s patentable subject
matter.
Benson translated one symbol into another symbol with the
identical interpretant. Flook manipulated one set of symbols and transferred the
result to the production process as alarm limit symbols with different
interpretants. Diehr used the novel process to produce referents; precision,
cured-rubber components. It did not matter that the actual referents, say rubber
ducks, were symbolised in the process. It mattered that, once the process was
finished, the process produced significant referents as claimed in the
patent.
So, why was Bilski abstract ideas? The process provided a
symbol set to guide the middle man. It did not result in a new referent or
referent set. As the courts should always do, §101 was considered first and the
invention was ruled out as unpatentable subject matter because it was abstract
ideas. If the court had gone on to consider the other sections, they would have
found that the only novel concept was the math algorithms used. Hedging and
dealing in the energy market were prior art. The math algorithms were non
patentable subject matter and also prior art because the courts treat all
math as prior art no matter how novel it may be. From the quotation,
above,The Court concluded that the process at issue there was
“unpatentable under §101, not because it contain[ed] a mathematical algorithm as
one component, but because once that algorithm [wa]s assumed to be within the
prior art, the application, considered as a whole, contain[ed] no patentable
invention.
If the execution of a computer program results in
symbols being displayed on a screen, printed on paper or stored in a medium,
that is not the production of referent.
Let's consider a system
comprising a computer and a mixing desk used to record music and duplicate a
music CD of the music. The music CD is the referent being produced. I doubt that
there is a patentable novel invention in there, but, if there was, it would have
to be the whole process of recording the performance and duplicating the CDs and
not just the burning of CDs.
Without the music recording process,
running the program to burn several music CDs is no different to copying any
data file to any CD. It is only the tying-in of the recording of the music file
into the invention that provides any potential for referent production. '[T]he
prohibition against patenting abstract ideas “cannot be circumvented by
attempting to limit the use of the formula to a particular technological
environment. or adding “insignificant postsolution activity.”' It does not
matter how often the symbols are transferred from one sign vehicle (the file) to
another sign vehicle (the CDs) no referent has been involved. Narrowing the
invention to just symbols representing music does not change this into
patentable subject matter.
Looking at the 'swipe to lock' invention, a
swipe of a finger and 'locking' are two abstract ideas. In a touch-screen
device, a programmer may put symbols into his program that represent a
particular sort of finger swipe across the touch screen panel and narrow the
'locking' symbol to 'preventing some or any physical buttons on the device, or
symbols representing the actions of physical buttons, initiating their symbol
manipulative actions'.
A finger swipe and a button operation cannot be
signs in a computer program. They can only be represented by signs. The
interpretants of those two signs will only be known to the programmer, unless he
adds program comments to share the interpretants with other programmers. The
programmer can only manipulate those and other symbols in the computer.
This particular program can only be modelling the finger swipe and
button push referents. Abstract ideas cannot be patented and the modelling of
abstract ideas or anything else by manipulating symbols cannot infringe on a
valid referent-based patent.
A programmer cannot create referents by
manipulating signs from the sign-interpretant-referent triad. Only by tying
other specific systems with the smartphone and having the process encompassing
the program generate a referent such as a precision rubber product can the
overall process have any potential for patent protection. The program in the
smartphone is not such a process/method as a stand-alone device. Nor is it a new
machine in its own right.
The invention, without limiting the
manipulation of the symbols to a particular technological environment, is just
abstract ideas. One can neither have a box of finger swipes nor a box of
locking. Limiting the abstract ideas to the technological environment of a
touch-screen device is only possible if a programmer redefines the symbols to
make sense in that technology. The symbols created by the programmer are not the
abstract ideas in the patent. Therefore, they cannot infringe on the patent even
if the patent were valid, which it cannot be.
It is worth repeating
that patents cannot be infringed upon by just 'doing things' even if it is doing
things with a smartphone or doing things in programs. Only the manufacture,
importing, selling or using of machines, following processes, executing methods
and transforming of materials can infringe on patents.
What if the
touch-screen device was not a mobile phone? What, in the invention, is to be
locked? If the patent had said 'the iPhone has a lot of virtual buttons that do
stuff. I want to monopolise the concept of disabling some or all of those
virtual buttons when used on a touch-screen phone' then it would have been
obvious that the invention was bogus.
Applying the science of computing
and the philosophy of semiotics, any invention to do solely with the
manipulation or the modification of the manipulation of symbols cannot, by
definition, act on referents and is both math (manipulation of symbols in a
computer) and abstract ideas (the selection of symbols shared between the
inventor and the user) and is non-patentable subject matter on both
counts.
The philosophy of semiotics fits the cornerstone patent
decisions of the Supreme Court and provides the intellectual backing to the,
hitherto, pragmatic decisions of the court ('Indeed, all members of the Court
agree that the patent application at issue here falls outside of §101 because it
claims an abstract idea').
How very
satisfactory!
---
Regards
Ian Al
Software Patents: It's the disclosed functions in the patent, stupid! [ Reply to This | # ]
|
| |
| Authored by: Ian Al on Sunday, December 02 2012 @ 04:28 AM EST |
Once there were two camps of artist; the figurative artist and the abstract
artist. Art is the manipulation of paints, pencil or charcoal to produce the art
which may be symbolic of something real or it may be abstract.
That's when it is not sculpture. Or performance art. Or an installation.
The figurative paintings are symbols conforming to the semiotics triad. However,
the symbols are not what they seem. Magrite painted a picture of a pipe entitled
"Ceci n'est pas une pipe" - 'this is not a pipe'. The painting was a
symbol of a pipe. The interpretant is not 'a pipe in the mind of a viewer'.
There is no referent. The painting and the title of the painting are essential
components of the painting. The interpretant of art is in the eye of the
beholder.
It is not possible to patent the method or process that an artist uses, because
it cannot be completely expressed in patent claims. The art is only protectable
by copyright because it is creative expression. It is not a manufactured
machine.
The artist might create an expressive work of art by arranging an unmade bed, or
a tent with the names of previous lovers pinned inside (Tracey Emin). Another
artist may 'paint' by trickling paint in a stream from a paint can or splashing
paint from a brush (Jackson Pollock).
Computer artists have used the computer screen and mouse as canvas, paintbrush
and palette. Other computer artists have programmed the manipulation of shapes
and colours by using computer language programs executed by the computer. Yet
more have provided the facility of tactile surfaces for the viewer to interact
with the art. Again, the bed, the tent, and the computer are not the referent
nor the interpretant. Often the title is an essential part of the art.
As the exercise of the law in the US lower courts stands, what a programmer
makes visible on a computer screen or printer, or audible via the speakers is
patentable as long as the symbols in the sign-vehicle that he manipulates have a
fixed interpretant and a fixed referent.
The vital legal question that the courts fail to put is 'is it art?'. If it is
art then it is non-statutory subject matter.
If it is the mathematical manipulation of symbols or the symbolising of abstract
ideas in a real medium whereby the signs have a specific interpretant and
referent , then, in the eyes of the lower court, it is patentable, statutory
subject matter. This is even though both abstract ideas and mathematical
manipulation of symbols are ruled non-statutory by the Supreme Court.
The lower courts are ruling that if the symbols manipulated in a program have
the same interpretant and referent as the symbols claimed in a patent, then the
patent is infringed even if the programmer had no intention of using symbols
with the same interpretant.
The only interpretants in source code are those formed by using the source code
computer language. The patent system has precluded the programmer from using any
symbols in his program that have the same interpretant set and are manipulated
in the same way as the claims in a patent.
When it comes to evaluating whether the programmer has used the symbols and
symbol manipulation in his program that is protected by the patent, then the
judge or jury decide on the basis, not of the symbols used and manipulated, but
whether it looks like it to the lay person.
---
Regards
Ian Al
Software Patents: It's the disclosed functions in the patent, stupid![ Reply to This | # ]
|
| |
| Authored by: Anonymous on Sunday, December 02 2012 @ 08:58 AM EST |
10 PRINT CHR$(205.5+RND(1)); : GOTO 10
examines the nature of software.
It is reviewed by Slate at:
http://www.slate.com/articles/technology/books/2012/11/computer_programming_10_p
rint_chr_205_5_rnd_1_goto_10_from_mit_press_reviewed.html
From the book:
"Computer programs process and display critical data, facilitate
communication, monitor and report on sensor networks, and shoot down incoming
missiles. But computer code is not merely functional. Code is a peculiar
kind of text, written, maintained, and modified by programmers to make
a machine operate. It is a text nonetheless, with many of the properties of
more familiar documents. Code is not purely abstract and mathematical; it
has significant social, political, and aesthetic dimensions. The way in which
code connects to culture, affecting it and being influenced by it, can be
traced by examining the specifics of programs by reading the code itself
attentively.
Like a diary from the forgotten past, computer code is embedded with
stories of a program’s making, its purpose, its assumptions, and more. Every
symbol within a program can help to illuminate these stories and open
historical and critical lines of inquiry."
Free download from: http://10print.org/ Creative Commons licence[ Reply to This | # ]
|
| |
| Authored by: Anonymous on Wednesday, December 05 2012 @ 09:31 AM EST |
You start with a distinction of different aspects of patentability of software.
The article would in my opinion profit from making these distinctions more clear
and where your argument stands.
These distinctions by the way also apply to other forms of "intellectual
property"; obviously, one must make the
1. Ethics / morals. There are different opinions on the ethics of IP
protection.
E.g. Ayn Rand would say that intellectual property is, like property in general,
some sort of sacred "natural right" and society should try to honor IP
as much as possible.
E.g. Stallman would say that "information wants to be free" /
computation and information sharing is a human right and society should try to
honor IP as little as possible.
E.g. the US constitution seems to take the same view as Stallman (but is willing
to take different compromises). This is ideology and not politics.
2. Utilitarian. Which does benefit society more?
There are good arguments for either conclusion on calidity of IP. Luckily, this
is mostly an empirical question and not a moral one- so it is for scientists to
decide, not for judges or politicians.
3. Compromise. After the first two questions are decided, a compromise must be
reached. That's politics.
4. Coherence. Whatever compromise society is going to make should not be too
contradictory- but some contradictions are OK. Compromise again.
5. Existing Law. IANAL, so this is for you.
You seem to argue that "software patents are valid" and
"mathematics is not patentable" are contradictory statements.
Even more, you seem to argue that "there exist valid patents" and
"mathematics is not patentable" are less contradictory than the first
pair of statements and we therefore lose coherence by such a state of affairs.
I see three immediate problems with your argument.
1. You do not argue, why the contradiction is so bad. Sometimes two rules clash;
so what?
2. Your argument does not make it clear, where computers/ computer programs are
different from e.g. a windmill. A physicist might see
"windmill" = "laws of nature" + "abstract maths"
"computer program" = "abstract maths"
Since "laws of nature" are not patentable and the relevant and known
ones fit on a single sheet of paper anyway (and are discovered for more than 30
years), the difference is not obvious.
3. Your coherence argument contains at its core something like "there is no
coherent rule separating abstract ideas and software patents". You use
arguments like "the interpretation of voltages is up to human
interpreters".
This lacks imagination on how complex and still coherent a rule might be. For
example, the interpretation of voltages is a single bit. You do not need to know
the charset used by a text-outputting program in order to interpret it: This is
just a Cesar's chiffre, which is easily crypto-analysed.
Software which is reverse-engeneerable does not need to carry context with it,
it is self-interpreting.
Or, in a different notation: (Compressible) Data does not need context
(conventions for human interpreters) in order to be understood. Good reading:
wikipdia "Kolmogorov Entropy".
[ Reply to This | # ]
|
|
|
|
|



