What Does "Software Is Mathematics" Mean? - Part 2

A Semiotics Approach to the Patent Eligibility of Software

by PolR

[This article is licensed under a Creative Commons License; article as PDF.]

I argued in part 1 of this series that computations are manipulations of symbols with meanings. In this article, I hope to further explain this notion using the social science of semiotics. Its object is the study of signs, the entities which are used to represent meaning.

This article elaborates on what Richard Stallman said in the recent Santa Clara Law conference Solutions to the Software Patent Problem.

According to this report Richard Stallman described patents on software as patents on thought, which amount to patents on the use of the human brain to reason and to solve problems by the application of reasoning. This article uses semiotics to show that Stallman's point is more than rhetoric. It is a provably correct statement of fact.

There may be patents involving software which don't privatize human thoughts but the current interpretation of the law doesn't draw a meaningful line. The Federal Circuit in CLS Bank International vs Alice Corporation complained that no one understands what makes an abstract idea abstract.¹ In this article I argue that semiotics is the correct framework to draw this line. The knowledge of semiotics let us distinguish when an advance over the prior art is an improvement in the human understanding as opposed to a new and nonobvious application of the physical properties of computer hardware.

In part 1, I argued that a test based on manipulation of symbols would correctly identify the abstract ideas in software. In this article, I will attempt to show how such a test could draw the line where it belongs according to semiotics. This should answer the questions asked by the Federal Circuit when they granted en banc review of CLS Bank vs Alice.

a. What test should the court adopt to determine whether a computer-implemented invention is a patent ineligible "abstract idea"; and when, if ever, does the presence of a computer in a claim lend patent eligibility to an otherwise patent-ineligible idea?

b. In assessing patent eligibility under 35 U.S.C. § 101 of a computer-implemented invention, should it matter whether the invention is claimed as a method, system, or storage medium; and should such claims at times be considered equivalent for § 101 purposes?

Summary of the Argument

[The article is based on the works of Professor Kevin Emerson Collins. See Semiotics 101: Taking the Printed Matter Doctrine Seriously, Kevin Emerson Collins | 85 Indiana Law Journal 1379 (2010) ( PDF ).]

In semiotics, a sign is a sign when it has a semantics defined by conventions. Interpreting a sign according to the conventions is a faculty of the human mind. This faculty is what must be protected from privatization.

A sign has three components which must be distinguished. There is the sign-vehicle which is the physical occurrence of the sign. There is the referent which is the actual thing which is referred to by the sign. And there is the interpretant which is the idea a human interpreter would form in his mind when interpreting the sign according to its defining convention. For example marks of ink on paper forming the letters CAT are a sign-vehicle. The corresponding feline animal is the referent. The idea of a cat a human being may form in his mind is the interpretant. The combination of all three elements is the sign.

Programmed computers are sign-vehicles. The data stored in computers is defined by conventions which must be interpreted by humans. In part 1, I showed three examples of such conventions.

1. There are conventions which assign to voltages in wires a bit value 0 or 1. The same boolean gate doing the same electrical activity on voltages will perform either as an AND gate or an OR gate depending on which convention is used to interpret the voltages.

2. There are conventions on how series of bits read as numbers. The same arithmetic circuit manipulating bits in the same manner will perform different operations of arithmetic depending on whether the numbers are in unsigned or 2's-complement format.

3. There are conventions on which non mathematical meanings the numbers will stand for. The same arithmetic circuit will compute 1+1=2 or 1 apple + 1 apple = 2 apples or even 1 lawyer + 1 lawyer = 2 lawyers depending of the convention which is used.

This shows the functions of software are not performed through the sole physical properties of electrical circuits. The human mind plays a role because semantics is not built into the physical structure of the hardware. The functions of a programmed computer depends on the conventions used to interpret the data. This is like a clock. The clockwork is a patentable mechanical device but it cannot fulfill its functions without a convention on how to interpret the position of the hands.

This simple fact exposes one of the errors in the doctrine that programming a computer makes a new machine. In theory this doctrine purports to patent inventions whose functions are performed though the physical properties of electrical circuits. In practice it permits patents on interpretants. It is used to justify exclusive rights on thoughts and logical processes in the human mind.

If we choose to view a computer as a machine that processes electricity independently from the human mind there is no semantics. We only have meaningless electrical phenomenons like voltages, charges and currents. Programming a computer is not a nonobvious improvement over the prior art without semantics. Storing meaningless electrical charges in the capacitors of main memory is a well known procedure.

Programming a computer requires defining the data. The programmer must define the conventions on the syntactic organization of the bits and the corresponding semantics. Then he must define the operations of arithmetic and logic which will solve the problem. This is all interpretants. This is all thoughts in the programmers' minds.

Collins' article discusses how semiotics applies to software. In doing so he makes two errors. The first one is he accepts the doctrine that programming a computer makes a new machine. The second one is he considers only the point of view of the end user. He pays no attention to the point of view of programmers and computer engineers. He believes the information stored in the computer which is not visible to the end user does not have a semantics in the sense of semiotics. This is incorrect, Computer programmers routinely examine the internal states of computers with debugging tools. They interpret the meaning of the hidden data when doing so. Besides, the three example of conventions from above apply to all data whether or not it is visible to the end user. The internal state of a computer is a sign because it has a semantic meaning defined by human conventions.

The same conclusion may be reached from reading the words of a patent. The disclosure of a software patent typically requires the programmer to interpret the computer as a sign in order to reproduce the invention because the functions of the software are defined in terms of the meaning of the data. Also, when the claim recites the meaning of the data, we need to interpret the computer as a sign to determine infringement.

Once Collins' errors are corrected his article gives us a precise description of what is an abstract idea in software. If the invention is a sign and the only nonobvious advancements over the prior art are interpretants then the claim is directed to an abstract idea.

Summary of Part 1

Let's have a short recapitulation of part 1. This will refresh our memory before we move to the main topic.

Mathematical Algorithms Are Procedures for Manipulating Symbols

A computation is a manipulation of symbols conveying meanings. This manipulation is described by a procedure called an algorithm.

At the hardware level, stored program computers execute computations using a procedure called the instruction cycle. This procedure works as follows:

1. The CPU reads an instruction from main memory.

2. The CPU decodes the bits of the instruction.

3. The CPU executes the operation corresponding to the bits of the instruction.

4. If required, the CPU writes the result of the instruction in main memory.

5. The CPU finds out the location in main memory where the next instruction is located.

6. The CPU goes back to step 1 for the next iteration of the cycle.

As you can see, the instruction cycle executes the instructions one after another in a sequential manner. In substance the instruction cycle is a recipe to "read the instructions and do as they say".

This procedure manipulates symbols because it manipulates bits and bits are symbols.

This procedure is also an example of what is known in computation theory as a universal algorithm. This is a subcategory of algorithms mathematicians have found. Universal algorithms have the capability to compute every function which is computable. If we give this algorithm a program as input it will compute the corresponding function.

Several universal algorithms are used in computer programming. Some of them, like bytecode interpreters, are implemented in software. The most often used universal algorithm is the instruction cycle implemented in the hardware of every stored program computer. The notion that all computer programs are ultimately the execution of some universal mathematical algorithm is the factual basis of the slogan "software is mathematics".²

A Way to Design a Test to Identify Patent Ineligible Abstract Ideas

Mathematical algorithms are a subcategory of manipulations of symbols and manipulations of symbols are a subcategory of abstract ideas. I propose that the court should use a test based on manipulations of symbols to identify the abstract idea.

The basic principle is that a manipulation of symbols should be an easy to define concept. The Federal Circuit has found that terms like mathematical algorithm and abstract ideas are hard to define. But if we remove the definitional difficulty the biggest hurdle toward getting a workable test should be solved.

Details on how I believe the test should work will be found below in this article.

Some Elements of Semiotics

Semiotics is a social science dedicated to the study of signs. Law professor Professor Kevin Emerson Collins has suggested to use semiotics to reinterpret the printed matter doctrine as a sign doctrine. He says the printed matter doctrine actually curbs the reach of patent protection into mental representations in the human mind. According to Collins a semiotics approach is revealing both the conceptual coherence hidden in the printed matter doctrine's historical applications and the doctrine's as-of-yet unnoticed statutory grounding.³

The Triadic Notion of a Sign

Collins explains the basics of semiotics thus:⁴ (footnotes omitted, emphasis in the original)

Semiotics is the study of signs, and signs are entities that involve something standing for something else to somebody. To conceptualize the operation of a sign, Peirce and his followers posit a triadic model of the sign. They argue that every sign involves three distinct components: a sign-vehicle, an interpretant, and a referent.

The Peircean sign is commonly depicted as a triangle, as in Figure 2:

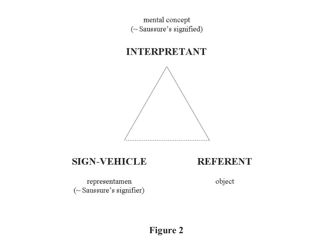
The sign-vehicle is the perceptible form of the sign; it is the physical artifact that an interpreter perceives. The particular combination of curves that make up the letter "S" and the formal properties of the dots, dashes, and blank spaces that make up a message transmitted in Morse code are both sign-vehicles, as are the undulating sound waves that convey the sound of the word "dog." The interpretant is roughly the concept that the sign-vehicle invokes in the mind of a person for whom the sign is meaningful. The referent of a sign is the thing in the world that is described, indicated, or referred to by a sign. Both interpretants and referents are within the ambit of the general term semiotic meaning as employed in this Article. For precision, a sign-vehicle will be described as signifying its interpretant and referring to its referent.

Peirce's sign "involves a rejection of the equation of 'content' and meaning; the meaning of a [sign-vehicle] is not contained within it, but arises in its interpretation" by an interpreter in the form of an interpretant. In other words, the sign-vehicle is not the sign, despite the commonplace nature of the language in which the material sign-vehicle is employed as a synecdoche for an entire sign. Stop-signs-as-artifacts -- the physical, red, octagonal things located at intersections -- are not signs in and of themselves. They are sign-vehicles and therefore only components of signs. The sign is the combination of the perceived thing (the sign-vehicle), the mental concept that the sign triggers in the mind of an interpreter (the interpretant), and the things or events in the world to which the sign refers (the referents). The sign-vehicle is a particularly useful term for the perceived component of the sign precisely because it wears on its sleeve a warning against the misleading synecdoche.

As you can see semiotics gives us the vocabulary to name with precision the constituent elements of a sign.

This triadic conceptions of signs is applicable to computer science and any other engineering discipline which involves computations. I think it is very insightful to see a sign not as a single indivisible entity but as a composite of constituent elements. It is also insightful to observe that an interpretant is an idea in the mind of the human interpreter. This is precisely the type of understanding we need to distinguish abstract ideas involving computations from concrete patent eligible inventions.

There is more on semiotics in Collins' article. If you are interested please read the whole article.

Signs Are Characterized by Social Conventions

In semiotics we must distinguish between causal relationships resulting from the action of physical phenomenons and semantical relationships resulting from social conventions. This distinction allows to recognize when something is a sign. Collins explains.⁵ (footnotes omitted)

Defined in the negative, a sign-vehicle is an entity that acquires meaning through a mechanism other than through deterministic cause and effect. It is "a physical phenomenon which provokes reactions in mechanisms and organisms, without being the cause of these reactions." The physical reactions provoked in interpreters by signs -- to the extent that there are any extroverted reactions at all by the interpreters -- are mediated by minds and mental states. In a positive manner, Eco defines semiotics to involve only the study of things that stand for other things by social convention. The key concept is that simply through a social agreement, the semiotic meaning of the stop sign can change.

Clearly, this distinction draws a boundary. We can apply it to the functions of computing machines such as programmable computers. On one side we have functions which are performed through the physical properties of the device. They involve some cause and effect relationships dictated by some laws of nature. On the other side we have functions which are performed through an operation of the mind of an interpreter. This operation associates meanings to sign-vehicles. It is defined by agreements between humans.

This boundary is one possible way to distinguish between abstract ideas and concrete inventions. Sometimes we may have a claim written to a sign-vehicle where the only nonobvious advancement over the prior art is the meaning of the sign. The innovation is entirely an understanding in the human mind, an interpretant. These claims are written to abstract ideas. Collins reinterprets the printed matter doctrine in this manner.

The data processing functions of a computer also lie on the semiotic and abstract side of the boundary. The evidence has been documented in part 1 of this series of articles. Let's recapitulate the main points. Please note how the meanings may change according to how humans define conventions. This is how we recognize when a sign is indeed a sign.

• The first evidence is the ability of the engineer to decide whether a given voltage means the bit 0 or the bit 1. Depending on his decision the exact same circuit manipulating the exact same voltages will carry out a boolean AND or a boolean OR operation. The difference is not physical, it is in the perception of the engineer and it is controlled by a convention. In semiotic terms a bit is a sign with three components. The abstract symbol 0 or 1 is an interpretant, the voltage representing the bit is a sign-vehicle and the corresponding truth values and numbers are the referents.

• When a circuit for addition adds 10000000+01111111 resulting into 11111111 it could mean either 128+127=255 in unsigned integer format or -128+127=-1 in 2s-complement format. At the physical level the same circuit manipulates the voltages in an identical manner. The difference is in the syntax the user has chosen to represent the numbers. This shows that one cannot reasonably argue the numbers are part of the physical structure of the computer. They are part of how human beings understand the activity of the computer. They are interpretants determined by the choice of a syntactic convention.

• There is also the semantical relationship between bits and numbers on one side and the real world referent on the other side. This too isn't a physical property of electrical circuit. For example the difference between 12+26=38 and 12 apples + 26 apples = 38 apples isn't a difference in the physical properties of a calculating machine. It is a convention on how the numbers should be interpreted. Once again the association of numbers with real life things is a decision of a human.

In all of the three examples the exact same circuit doing the exact same electrical activity actually performs different functions depending on how the engineer or programmer choses to interpret it. This is the key. Semantical relationships are determined by social agreements. They are choices that may be changed. Humans would not have the option of changing these choices had the functions been performed through the physical properties of the circuit.

The Functions of Programmed Computers Depend on Human Understanding

The alternative view is to treat the computer as a machine for manipulating voltages in wires, electrical charges in capacitors and magnetic moment on hard disks. It will happily perform its functions whether or not someone is looking at the meanings of data. Think of an anti-lock brake system. The embedded computer will make the car brake without locking the wheels in absence of a human observer. In this sense the computer performs its functions according to the laws of physics.

This view omits semantics. We may defend it when the functions of the circuit don't require the physical phenomenons to have meanings. Otherwise we have three counterexamples: the interpretation of voltages in boolean gates, the representation of the syntax of numbers and the non mathematical meaning given to mathematical entities. These three examples cover the most fundamental element of computing: the representation of data. The functions of software depends on the knowledge of the conventions used to represent the data. This is not an physical property of an electrical circuit. In the three counterexamples we have the exact same circuit operating physically in an identical manner and they perform a different function when the conventions are changed.

Let's consider what happens when we introduce a program into a computer. The program itself is data. It is stored as electrical charges in capacitors located in main memory.⁶ Each charge represents a bit. Instructions are series of bits to the intention of the instruction cycle. The CPU will read these bits instruction by instruction and perform the corresponding operations.⁷ When viewed this way it is tempting to argue that the interpretant is irrelevant. The behavior of the computer is dictated by the physical properties of the electrical circuit. Collins actually defends this thesis:⁸

To understand the irrelevance of the interpretant, consider a hypothetical in which human understanding is taken out of the picture. Even if humans did not understand the genetic code, an isolated and purified gene would be patentable because it could be used to provoke a cell to produce a protein. Similarly, software on a disk is an advance over the prior art because its structure causes a computer to exhibit a particular behavior. Even if computer programmers forgot how to read and understand a programming language, the computer software recorded on a disk would remain patentable because it would still cause the machine to exhibit a specific behavior.

Let's see how this thesis works out in reality. Let's assume we have a program for managing reservation in a conferences. We received 128 reservations from the web site and 127 reservations through regular mail. The program contains an instruction to add the two numbers: it adds 128+127 for a total of 255 reservations. What is exactly the particular behavior of the computer while it executes this instruction, assuming the human understanding is taken out of the picture?

Without human understanding we don't know whether a particular voltage in a wire is the bit 0 or the bit 1 because this is defined by a convention which must be interpreted by a human. The circuit processes meaningless electricity. This is not performing the functions of software.

Let's ignore this point and assume we may see the computer as a machine for manipulating bits. Then, the instruction adds 10000000+01111111 resulting into 11111111. Without human understanding how do we know this is 128+127=255 instead of -128+127=-1? Electrically speaking this is the same machine behavior. The same adding circuitry processing the same bits will perform both additions depending on whether the programmer decided to use unsigned arithmetic or 2s-complement arithmetic. The instruction triggering this addition is exactly the same in both cases. The difference lies solely in the intent of the programmer.

Let's ignore the two preceding points. Without human understanding how do we know the numbers 128, 127 and 255 refer to reservations to a conference? How do we know they aren't a count of apples in a grocery inventory program? This knowledge is not built into the electrical structure of the machine. Once again there is no observable difference in electrical behavior.

The information processing functions of a computer cannot be separated from human understanding. A programmed computer is a sign and the computer hardware is a sign-vehicle. The thesis that interpretants are irrelevant to the computer behavior is not tenable when the behavior is defined in terms of manipulation of bits, numbers and logical operations on their meanings. Interpretants are irrelevant only when the behavior is defined in terms of meaningless physical phenomenons.

New Nonobvious Interpretants Are Patent Ineligible Abstract Ideas

The draftsmen of patents have a choice. They may describe the behavior of computers solely in meaningless electrical terms. Then interpretants are irrelevant to this purely electrical behavior. They may also describe the behavior in terms of data processing. Then the interpretants are relevant because they are recited in the patent.

If a patentee considers the computer as a machine for manipulating voltages can he patent it? Before answering this question I would ask, is there a nonobvious advancement in the manipulation of meaningless voltages? If so the claim must recite this advancement to be granted.

If the only advancements over the prior art are interpretants,
the invention is an abstract idea in the mind of the interpreter.

An old fashioned mechanical clock may provide a good analogy. Put the clock in a dark room where nobody goes and it will keep time unattended. The clockwork performs its functions according to the laws of physics whether or not someone watches it. But time can only be read by a human interpreting the position of the hands. This is a semantical relationship.

The convention for reading time may be changed. This makes the clock a sign according to semiotics. For example, suppose we decide to use a decimal time system. In this system there are 20 hours in a day, 10 before noon and 10 after. Each hour is divided in 100 minutes and each minute is divided in 100 seconds. We can easily build a clock that keeps time according to this new system. We just have to paint the numbers 1 to 10 on the old clock in place of the old numbers. Then the position of the hands can be interpreted according to the new convention. The short handle indicates the hour and the long handle indicates the minutes if you mentally multiply the numbers by 10.

Here is the abstract idea question. Did we invent a new clockwork which performs its functions according to the law of physics? Or did we invent a new way to interpret the meaning of an old clock? Of course, in the decimal clock example the clockwork was not changed. The invention amounts to painting new numbers on the clock.

This is not inventing a new clock.

A programmed computer is like this clock. If we omit the semantic and consider only the physical properties of the circuit there is no new and nonobvious element in a programmed computer. The electrical circuit always carry out the instruction cycle. The program is electrical charges stored in main memory. There is nothing new and nonobvious in storing meaningless electrical charges in memory. Besides, the contents of memory is modified billions of times per second as the computation progresses. The configuration of main memory is a moving part of the machine.

At the electrical level, then, programming the computer doesn't make a new machine.⁹

Programmed Computers Are Interpreted by Programmers

When debugging a program, a programmer will examine the data using debugging tools to verify its meaning. Software implements operations of logic. The software performs its functions only when the data manipulations are logically consistent. The task of debugging is to verify this is the case and correct any error.

There is an alternative view where the computer is a device for producing sign-vehicles. In this view, only the input and output visible to end users are signs. The internal states of computers are not considered to be signs because they are not visible to the end user. This view fails because it doesn't take into account that the internal state is visible to programmers. End users are not the only human beings able to interpret signs in a computer.

For a programmer, an unattended computer is like a book sitting on a shelf. This book isn't currently read but its meaning is available to whoever opens it. Similarly, no one checks the internal state of a programmed computer once the program is done debugging. But programmers know that if they inspect it they will read the meanings.¹⁰

The implication is that the internal activity of a computer is a sign even when it is not actually examined by a live human. This is the correct result. According to semiotics, a device is a sign whenever there is some convention on how to interpret its meaning. The requirement is not that someone actually applies the convention. It is that the convention must be defined. Then if someone comes along and uses the convention, the meaning could be understood.

Defining the conventions which make a programmed computer a sign is part of computer programming. The programmer defines how the data is represented and what is the semantics. The programmer defines the operations of arithmetic and logic the algorithm must carry out. The computer performs its functions precisely because the electrical activity of the computer is a sign-vehicle. This activity represents the correct operations of logic when the data is interpreted according to the conventions. When this is not the case, the software has a bug. It produces the wrong answer. The programmer must then inspect the internals of the computer to determine where the error is. This procedure requires him to analyze the semantics of the internal computer activity. In other words, the computer must be interpreted as a sign.¹¹

This situation is typically reflected by the words of a patent. The disclosure mentions the data definition and the operations of arithmetic and logic. The implementer who follows the disclosure is required to interpret the computer as a sign. The claim similarly recites the data definition and the operations of arithmetic and logic. The computer must be interpreted as a sign when determining whether the claim is infringed.

The opposite view -- that there is no sign unless someone must actually watch the sign-vehicle -- leads to absurd results. A book sitting on the shelf would not be not a sign until it is opened and read. A DVD containing a movie picture would not be a sign because no one actually looks at the bits on the disk in their compressed format.¹² Cuneiform tablets buried in the sands of the Mesopotamia would not have been signs during all these centuries where the ancient Sumerian language was forgotten.

The Courts Should Stop Using the "New Machine" Doctrine

According to a long-standing series of precedents, programing a computer makes a new machine distinct from the unprogrammed computer. I argue that this doctrine prejudges the outcome of the analysis which must be made. When the claim is directed to an abstract interpretant no new machine is made.

The courts have explained why they have adopted this doctrine in several ways. Here is how they explained it in In re Noll (November 18, 1976),

There is nothing abstract about the claimed invention. It comprises physical structure, including storage devices and electrical components uniquely configured to perform specified functions through the physical properties of electrical circuits to achieve controlled results. Appellant's programmed machine is structurally different from a machine without that program.

We have just seen that this is false. Semantics is not a physical property of an electrical circuit.

Sometimes people argue that programming a computer makes a new machine because the functions of the computer are new. This argument takes for granted that the functions of software are performed through the physical property of the circuit. What if these functions are performed through conventions on how to interpret the meaning of the data? In such case the invention is an interpretant in the mind of the programmer. The machine is not changed just because we understand it differently.

The "new machine" doctrine is factually incorrect. Also, this doctrine precludes the conclusion that the invention could be an interpretant.

I protested that the "new machine" doctrine is technically erroneous in a preceding article. I have presented there several reasons why this doctrine is factually incorrect. I have also cited several cases where the courts have explained how they justify the "new machine" doctrine. All these explanations are based on erroneous interpretations of how a stored computer works. None of these explanations consider the role of semantics. They all assume the functions are performed as stated in Noll "through the physical properties of electrical circuits to achieve controlled results". We find more erroneous theories of this nature in the concurrent opinions of judges Rader and Newman in In re Alappat¹³ and also in an amicus brief submitted to the Supreme Court in Bilski v. Kappos.¹⁴

Lawyers say the "new machine" doctrine is a legal fiction.¹⁵ They say the courts understand programming a computer doesn't make a new machine. They say the courts don't mind making a legal fiction if they believe software is the type of invention which reasonably is within the scope of patent law and a fiction is necessary to achieve this result. In this case I wonder why the courts believe it is reasonable to patent software in the first place. All indications I could find say that the courts believe what is said in Noll: that the functions of software are performed through the physical properties of electrical circuits. No independent justification appears to exist.

To put it different way, why would an interpretant reasonably fall within the scope of section 101 of patent law? Here is how this section reads:

Whoever invents or discovers any new and useful process, machine, manufacture, or composition of matter, or any new and useful improvement thereof, may obtain a patent therefor, subject to the conditions and requirements of this title.

The courts should stop using the "new machine" doctrine. It purports to grant patents on electrical improvements of the unprogrammed computer when no such nonobvious improvement occurs. It is nothing more than an excuse to confer patent rights to ideas in the mind of programmers.

How to Identify Abstract Ideas in Software Patents Using Collins' Proposed Sign Doctrine

Collins has proposed to apply semiotics to the printed matter doctrine. He has analyzed the core printed matter cases. He found that all these cases could be reinterpreted as what he calls the sign doctrine.¹⁶ (footnote omitted, emphasis in the original)

When the printed matter doctrine is reconceptualized in a semiotic framework and recast as the sign doctrine, the core printed matter cases can be seen to follow a simple rule: a claim that describes a sign is not eligible for patent protection if the sole locus of the nonobvious improvement over the prior art resides in a mental state. Semiotically framed, what courts are already doing under the banner of the printed matter doctrine -- but not what they are saying they are doing -- is invalidating claims that describe a sign in which the only nonobvious advance over the prior art resides in the processes that occur in the minds of interpreters. It is the interpretant of a sign, not the content of information more broadly, that cannot be given patentable weight.

Collins further explains the procedure:¹⁷ (footnote omitted)

The key to distinguishing permissible claims to signs from impermissible ones is not to inquire whether the patent claim describes a sign-vehicle but rather to determine whether what is novel and nonobvious is the semiotic meaning that a human interpreter should understand when she perceives a sign-vehicle. The semiotic framework for patent eligibility, therefore, focuses the exclusion from patentable subject matter not generally on meaningful things but specifically on improvements in human understanding itself.

I argue that this logic also applies to software. Just to be clear, I do not argue the printed matter doctrine applies to software. I argue that abstract ideas in a computer program are abstract precisely because they are interpretants. Therefore it makes sense to follow this sign doctrine. I also argue the human interpreter need not be the user of the software. He may be a programmer, a computer engineer, anyone who attempts to reproduce the invention from the disclosure or even an expert witness analyzing the invention to determine infringement.

Collins argues his doctrine requires a patentable-weight approach because otherwise it is not possible to identify claims written to abstract ideas when the claim is written to a sign. On the other hand the courts prefer to use a claim-as-a-whole approach when analyzing section 101 subject matter. The difference is this. In a patentable-weight approach the claim is patent eligible only when there is a nonobvious advancement over the prior art outside of the interpretants. This requires to consider the novelty and obviousness of individual claim elements during section 101 analysis. But in a claim-as-a-whole approach novelty and obviousness must be left out of section 101 and deferred to the analysis of sections 102 and 103.

Collins solves this dilemma by narrowly limiting his proposed sign doctrine to signs. Then claims are still analyzed with the preferred claim-as-a-whole approach except in those limited circumstances where it doesn't work.

Collins explains:¹⁸ (emphasis in the original, footnotes omitted)

First, on a conceptual level, the semiotic framework explains why it is appropriate for the patentability of an artifact to hinge on the content of the prior art and thus the historical context in which an invention was made. There is no reason to expect patent eligibility to be an intrinsic property of an artifact in a semiotic framework. Semiotic meanings are not intrinsic properties of artifacts. Semiotic meanings are not contained within artifacts; sign-vehicles do not have "content" in the sense of meanings contained within them. Printed matter is meaningful only because of the mental process of interpretation in the mind of an interpreter. Signs, not sign-vehicles, are the entities within which meanings reside. If a single component of a sign is artificially cabined off from the sign's other components -- for instance, if the sign-vehicle is examined in isolation -- it should be unsurprising that its eligibility for patent protection depends on something other than that single component's intrinsic properties.

To understand the value of a patentable-weight approach to the doctrine of patent eligibility in the context of semiotically meaningful things, consider the absurd results of taking a claim-as-a-whole approach to patent eligibility seriously. In other words, consider a hypothetical sign-as-a-whole approach to patent eligibility. Under a sign-as-a-whole approach, courts would have to take note of all of the components of a sign -- the sign-vehicle, the interpretant and the referent -- every time an inventor claimed a sign. If any of those individual components described patentable subject matter, then the claim as a whole would describe patentable subject matter. Because every sign has a perceptible sign-vehicle that is an extra-mental thing, every sign would be eligible for patent protection under the sign-as-a-whole approach. Despite their insistence on a claim-as-a-whole approach to patent eligibility, courts have understandably never shown interest in a sign-as-a-whole approach. Such an approach would not reach normatively acceptable ends. Only a patentable-weight approach can effectively prevent the privatization of advances in human understanding.

This argument is applicable to software because a programmed computer is a sign. Software patents as they are currently granted privatize advances in human understanding. Collins' proposed sign doctrine would end this practice.

A Test For Patent Ineligible Abstract Ideas

I have proposed to design a test based on manipulation of symbols. I now argue that this test is a good way to apply the sign doctrine to software patents. A programmed computer is a sign because bits are symbols with meanings. An analysis of the manipulation of symbols will correctly identify software patent claims where the sole nonobvious improvement over the prior art are interpretants.

The test works in three steps. Together they ensure Collins' proposed sign doctrine is narrowly applied to signs as per his recommendation.

1. The first step identifies whether data, semantics and operations of logic or arithmetic are recited in the claim. If so the claim recites a sign and we go to the next step. Otherwise the sign doctrine is not applicable.

2. The second step identifies whether the claim is written to the sign as opposed to something which merely uses a sign as one of its elements. Insignificant element of the claim must be disregarded in this analysis in accordance to Parker vs Flook and Mayo Collaborative vs Prometheus. The claim is deemed to be written to the sign when the utility of the claim as a whole is the substantially same as the utility of the sign taken in isolation. The assumption is that significant elements will substantially alter the utility of the claim while insignificant ones will not. If the claim is written to a sign we go to the next step. Otherwise the sign doctrine is not applicable.

3. The third step is to apply Collins' proposed sign doctrine using a patentable-weight approach. The claim is patent eligible only if there is a new and non obvious advancement over the prior art outside of the interpretants.

I will now walk through how this test should work. I will show that this test accepts claims that should be accepted and rejects claims that should be rejected. I use an anti-lock brake system as an example. This invention comprises the following elements:

• There are sensing devices which measure physical phenomena like the rotation of the wheels and the pressure the driver applies to the brake pedal.

• These measurements are sent to a microprocessor programmed with the anti-lock braking software.

• The microprocessor produces as output how much pressure must be applied on the wheels by the brakes.

• This output is received by an actuator which applies the pressure on the brakes.

This invention is not mere pushing around of the bits. I have chosen it because I think it put the proposed test under the maximum stress.

Separating Causal Relationships from Semantical Relationships

The first step of the test would be to determine whether the claim recites a manipulation of symbols. Any recitation of data, semantics, arithmetic or logical operations or even a general description of the functions to be achieved by the software would meet the requirements of this test This is a threshold step. If there is no manipulation of symbols the test is not applicable. Otherwise we can move to the next step. In the case of the anti-lock brake system, the outcome of this step depends on how the claim is written.

In one scenario the patent may be written in a language which doesn't refer to bits, numbers or the meanings of data. It only mentions physical devices and meaningless electrical phenomenons like currents and voltages. Perhaps the microprocessor isn't a programmable device. Perhaps it is a dedicated circuit and the patent recites how to make the circuit by assembling electronic components. An engineer who wants to reproduce the invention from the patent disclosure doesn't need to consider the meanings of the bits. He may just assemble the components and make sure the electric currents and voltages are as specified. Similarly, an expert witness in a lawsuit will determine infringement by examining the physical structure of the device without having to look at the meaning of the bits.

A patent like this is clearly written to an application of the laws of physics. It depends solely on causal relationships. There is no mention of sign and interpretants. People are free to implement an anti-lock brake system where a different circuit carries out the same computation. The sign doctrine should not be applied in this case.

Another scenario would sound like some customer entering a bookstore asking "I want this book about a hobbit traveling in far away countries where live elves and orcs. He wants to destroy an evil ring." These words are not describing an arrangement of physical marks of ink on paper. This request is: "I want the book which tells the story I am outlining." This is asking for a sign-vehicle by specifying its meaning. The patent may be written in that style. It describes the meanings of numbers measured by the sensors. The functions of the algorithm are described in terms of the meanings of the data. An engineer who needs to reproduce the invention must treat it like a sign. He must ensure the meanings are as stated in the disclosure. An expert witness in a lawsuit must also treat the invention as a sign. He must determine infringement based on whether the meanings recited in the claim are present.

This patent clearly recites some semantical relationships. People who implement an anti-lock brake system relying on the same computation may infringe on the patent. There is an issue of whether the advancements over the prior art is in the physical device or in a human understanding of an obvious combination of old physical elements. The first step is passed and we proceed to the next step.

The difference between the scenarios is what the patentee regards as his invention. If he believes it is an application of the laws of physics he can claim his invention in physical terms. But if he thinks the invention is about semantics he can claim it that way too. The test will be passed or not passed depending on how the claim is written. People are free to claim an anti-lock brake system which operates entirely according to the laws of physics and leave the interpretants out of the patent. And they are free to claim an invention involving an interpretant if they believe there is an element in the claim that distinguish it from an abstract idea.

Please note how the first step correctly separates patent claims which involve some semantical relationships from claims entirely relying on causal relationships. It distinguishes patent claims which involve signs from claims which don't.

Identifying Claims on the Referent

Assuming the claim passes the first step, the second step is to identify whether the claim as a whole is written to the sign or whether the sign is merely an element of the invention. In the latter case there must be at least one significant non-symbolic element. I use the word 'significant' because the analysis must comply with the requirements the Supreme Court has set forth in Flook and Mayo.

This second step too is a threshold step. If the claim contains at least one such element it is not written to a manipulation of symbols and the sign doctrine doesn't apply. Otherwise we move to the third and final step.

I think a semiotic framework allows to define precisely what 'significant' means. The non-symbolic elements are significant when the utility of the claim as a whole is substantially different from the utility of the sign taken alone. This is a recognition that signs may be useful. There are people who argue that claims on abstract ideas cannot be useful. I reject this view because claims on signs can both be useful and run afoul of the sign doctrine.

The analysis goes as follows. First we identify in the claim those elements which constitutes the sign. Then we identify what is their purpose, their 'utility' in patent-speak. Then we identify the utility of the claim when taken as a whole. If the two utilities are substantially different the non symbolic elements are significant and the claim is not written to a manipulation of symbols. Otherwise the claim as a whole does nothing more than the manipulation of symbols taken alone and the sign doctrine should be applied.

In the anti-lock brake system the sign element is the programmed microprocessor. Its utility is to inform us of how the brakes should be activated. This information is presented in the form of a series of numeric values representing the pressure which should be applied to the brakes at any given time.

The utility of the claim as a whole varies depending on which non-symbolic elements are recited. In one scenario the claim recites an element of actually applying the pressure on the brake. Then the utility of the claim is to actually brake the car in a non-blocking manner. This is substantially different from merely informing us of how to activate the brakes. This element is significant. The claim as a whole is not written to a sign and the sign doctrine does not apply.

In another scenario the claim doesn't include the element of actually braking the car. Many other non-symbolic elements may be added. There could be a mention of the sensors attached to the wheels and the wheels themselves. The sensors attached the gas pedal and the brake pedal may be recited. The claim may go as far as mentioning the car, the driver and the slippery road. But even when all these elements are included the utility of the claim as a whole is still to inform us of how the brake should be activated. The two utilities are not substantially different. The non-symbolic elements are not significant. The claim as a whole is written to a sign and the sign doctrine is applicable.

Please note how the difference between the two scenarios is related to the referent. In the first scenario the claim actually does what the sign means. This is the referent. In the other scenario this referent is only referenced as the meaning of the sign, it is not a physical element of the invention. This distinction is crucial. When the referent is not actually part of the claim a mere reference to it is an interpretant. But when the referent is actually present the invention is more than a mere thought in the human mind. An actual embodiment of the idea is claimed. This will show up in the test as a substantial difference in utility.

We see the same thing in the famous claim in Diamond v. Diehr. It includes the step of actually curing the rubber. The utility of the sign part of this claim is to let us know how long to cure the rubber. The utility of the claim as a whole is to actually cure the rubber. The referent is included. Omit the referent and this is only a claim on the abstract mathematical computation.

Collins explains that the Federal Circuit routinely ignores this distinction:¹⁹

[T]he semiotic framework suggests that the Federal Circuit should reconsider the routine patentability of newly invented computer models. When addressing computer models, the Federal Circuit today elides the sign-vehicle with the sign and therefore commits a classic semiotic error: it inappropriately reifies a newly invented semiotic meaning into a new intrinsic property of a tangible, extra-mental artifact. As a result, it sanctions a patent on a meaningful thing even when the only invention at issue resides in the mind of the person who understands the thing's newly invented semiotic meaning. Claims to newly invented computer models literally describe a programmed computer (a sign-vehicle), yet the only inventive aspect of the claimed technology may be a new mental state in the mind of a computer user (an interpretant).

This is the very point captured by the calculator experiment. Type in 12+26 on a pocket calculator. The result is 38. Now assume you add apples and type in 12 apples + 26 apples. The result is 38 apples. Do you see a difference in the calculator? Collins says the Federal Circuit grants patents on software based on the grounds that when this kind of semantics is given to a computer data they think a new machine is invented.

Identifying claims on Newly Engineered Physical Sign-Vehicles

Once a claim passes the first two steps and it is found that the sign doctrine is applicable there is one last step to be taken care of. Newly engineered physical sign-vehicles are considered patentable and I see no reason to consider them abstract. But this type of invention is not always distinguished from interpretants by the first two steps.

Consider for example a new method for encoding bits on a hard disk platter. This is a new technology for making hard disks. This invention should not be disqualified because bits may have meanings.

Let's consider a more tricky example, the Morse code.²⁰ This is a system for representing letters and numerals using tones, lights or clicks. It is written as physical marks shaped in the form of series of dots and lines separated by spaces. At the time of Samuel Morse this was a newly engineered sign-vehicle. A correct result of the test would be to allow a patent claim on Morse code which is limited to the physical representation of the symbols without claiming the actual text. On the other hand the test should bar a patent on Morse code which would have the effect of patenting the text.

Interpretants and newly engineered sign-vehicles may be distinguished using Collins' proposed sign doctrine. The claim is written to a patent ineligible abstract idea when the only nonobvious improvements over the prior art are interpretants. Collins mentions that the sign doctrine requires the use of a patentable-weight approach as opposed to a sign-as-a-whole approach. Interpretants should be given no patentable weight in the sense that they are not allowed to distinguish the claim over the prior art. But if something which is not an interpretant distinguishes the claim over the prior art then the patent may be granted.

A patentable-weight approach would give the correct result on a Morse code patent. Physical representations of letters and numerals are not ideas in the mind of human beings. They are sign-vehicles. A claim on a system to represent letters and numeral according to Morse code would be granted because at the time of Samuel Morse this particular sign-vehicle was a new and nonobvious advance over the prior art. It is suitable for use in telegraphic applications. On the other hand the text so represented is an interpretant. A claim directed to text written in Morse code would be rejected if the only nonobvious advancement is the encoded text.

The result of applying a patentable-weight approach to the anti-lock brake system depends on what exactly is being claimed.

In one scenario the claim may recite some new and nonobvious element of hardware. May be the sensors which measure the rotation of the wheel are an innovation. Or the microprocessor may use some new element of circuitry which is especially good at computing the anti-locking algorithm. These elements are not interpretants. They would be allowed to distinguish the invention over the prior art and the claim would be patent eligible. This is the correct result. People are free to implement the same computation when using different hardware while the inventor of the new hardware is granted his patent.

In another scenario the only new and nonobvious elements are the algorithm and the non-mathematical meanings given to the data. These elements are interpretants. They are not given any patentable weight and the claim will not be patent eligible. Again this is the correct result. The invention is thoughts in the human mind. It is abstract ideas.

Conclusion

Semiotics define concepts and vocabulary that let us state precisely what makes an abstract idea in a software patent abstract. When the only advance over the prior art is the syntax and semantics of the bits accompanied with the operations of arithmetic and logic, then the invention is an interpretant. It is a thought in the mind of programmers. This circumstance may be identified with a three step test limited to signs. It will not bar patent claims on inventions which are not signs. And it will bar patent claims on signs only when there is no invention outside of advancements in human understanding.

The doctrine that programming a computer makes a new machine conflates interpretants with physical improvements to computers. It should be abandoned.

Reference

[Collins 2010] Collins, Kevin Emerson, Semiotics 101: Taking the Printed Matter Doctrine Seriously ,

Indiana Law Journal, Vol 85, pp.1379-1443 (2010) (PDF). In this article, I assumed Professor Collins' explanation of semiotics 101 and his legal analysis of the printed matter doctrine are correct.

Footnotes

1 The exact complaint is: (emphasis in the original)

The abstractness of the "abstract ideas" test to patent eligibility has become a serious problem, leading to great uncertainty and to the devaluing of inventions of practical utility and economic potential. See Donald S. Chisum, Weeds and Seeds in the Supreme Court's Business Method Patent Decision: New Directions for Regulating Patent Scope, 15 Lewis & Clark L. Rev. 11, 14 (2011) ("Because of the vagueness of the concepts of an `idea' and `abstract,'… the Section 101 abstract idea preemption inquiry can lead to subjectively-derived, arbitrary and unpredictable results. This uncertainty does substantial harm to the effective operation of the patent system."). In Bilski, the Supreme Court offered some guidance by observing that "[a] principle, in the abstract, is a fundamental truth; an original cause; a motive; these cannot be patented, as no one can claim in either of them an exclusive right." Bilski II, 130 S. Ct. at 3230 (quoting Le Roy v. Tatham, 55 U.S. (14 How.) 156, 175 (1852)). This court has also attempted to define "abstract ideas," explaining that "abstract ideas constitute disembodied concepts or truths which are not `useful' from a practical standpoint standing alone, i.e., they are not `useful' until reduced to some practical application." Alappat, 33 F.3d at 1542 n.18 (Fed. Cir. 1994). More recently, this court explained that the "disqualifying characteristic" of abstractness must exhibit itself "manifestly" "to override the broad statutory categories of patent eligible subject matter." Research Corp., 627 F.3d at 868. Notwithstanding these well-intentioned efforts and the great volume of pages in the Federal Reporters treating the abstract ideas exception, the dividing line between inventions that are directed to patent ineligible abstract ideas and those that are not remains elusive. "Put simply, the problem is that no one understands what makes an idea `abstract.'" Mark A. Lemley et al., Life After Bilski, 63 Stan. L. Rev. 1315, 1316 (2011).

2 Please note what is NOT said. A program is not a mathematical formula. It is not argued software is mathematics because it could be described mathematically. There are people who believe the sentence "software is mathematics" means one or the other of the statements. This is incorrect and not the argument.

3 See the abstract of Collins article.

4 See [Collins 2010] pp. 1408-1411 (pp. 30-33 in the PDF)

5 See [Collins 2010] p. 1415 (p. 37 in the PDF). Also please note that this quote reflects Collins' view that a sign-vehicle is always a physical thing. I disagree. Intangible entities like mathematical symbols and numbers may also be sign-vehicles because they may have meanings defined by conventions. See part 1 of this series of article for the difference between a mathematical symbol and its physical representation,

6 This is assuming the computer uses DRAM technology for main memory.

7 Please note that the instructions by themselves do nothing. They are like travel directions written on paper. They don't drive the car. The driver does. The charges in main memory are just bits of data. The CPU is the active component doing the work. I feel the need to mention this because Collins quotes Pamela Samuelson thus: (See [Collins 2010] footnote 229 pp. 1421-1422, pp. 43-44 in the PDF)

There is one very simple but important difference between a book which contains a set of instructions about how to do a particular task and a computer program in machine-readable form which contains a similar, if considerably more elaborate, set of instructions on the same subject: The former informs a human being about how the task might be done; the latter does the task.

Programs don't do the task. Also programs in executable form are readable to programmers using disassemblers. This distinction doesn't match reality.

8 See [Collins 2010] p. 1422 (p. 44 in the PDF)

9 Collins discusses when a patent claim on a sign-vehicle may be granted. See [Collins 2010] p. 1424 (p 46 in the PDF). (emphasis added, footnotes omitted, )

Construed in semiotic terms, the printed matter doctrine states that a claim to a sign-vehicle is not eligible for patent protection if the sole locus of the improvement over the prior art resides in the interpretant that it signifies to an interpreter. The negative corollary of this limited rule is that there are many situations in which newly engineered sign-vehicles are eligible for patent protection.

For example, as already discussed, the negative corollary leads to the conclusion that newly engineered sign-vehicles are patent eligible when they have been engineered to possess non-semiotic properties in addition to their semiotic properties. Sometimes, the non-semiotic properties are structural properties of the sign-vehicle itself. A sheet of paper with a specific diagram printed on it is a sign-vehicle that is eligible for patent protection if the chemical composition of the ink in which the diagram is printed is a nonobvious invention. Sometimes, the nonsemiotic properties are the structural properties of the sign-vehicle that deterministically cause reactions in other systems. Newly engineered signals and stimuli are usually patent eligible for this reason despite the fact that they are frequently sign-vehicles as well. In either case, the advance over the prior art resides in a property other than the ability of the sign-vehicle to signify interpretants and, indirectly, refer to referents.

The structural- and functional-relation cases, which are traditionally viewed as exceptions to the printed matter doctrine, populate another category of newly engineered sign-vehicles that are eligible for patent protection under the negative corollary. Sign-vehicles have historically been patentable under the printed matter doctrine when they have been engineered so as to improve the efficiency of the process of signification without an accompanying improvement in what is signified.

Please note the criteria in bold. In software we have the opposite situation. A computer program is an improvement of what is signified without an electrical level improvement of the machine.

10 There are circumstances where the internal state of a computer used by the end-user will be inspected by a programmer. For example if a program crashes because of a bug, a memory dump may be taken and its contents may be inspected for debugging purposes.

11 I am insisting heavily on this point because lawyers often seem to assume that what is not visible to the end-user is not a sign. In particular, Collins makes this mistake. See [Collins 2010] p. 1421 (p. 43 in the PDF)

The binary ones and zeros recorded on an old-fashioned computer punch card or a newfangled USB drive are signals or stimuli: the mechanical or electronic devices into which they are fed are interpreters that, when functioning properly, produce responses through deterministic processes. No interpretants are required for software recorded on a disk to "mean" something in the nonsemiotic sense to a computer as an interpreter.

12 Video on a DVD is normally compressed to save space. This format cannot be directly displayed on a screen. The video must first be decompressed.

13 Here is an extract of judge Newman's concurrent opinion. Judge Rader's concurrent opinion on the same case contains a similar error. For the purposes of this article it suffices to quote Judge Newman:

Alappat's rasterizer is an electronic device for displaying a smooth waveform by selective illumination of pixels. The Alappat rasterizer operates by performing a sequence of steps in accordance with instructions that are generated electronically. This operation requires several mathematical calculations that are performed with the aid of microelectronic circuitry, and can be performed by a digital computer. The structure resides in the configuration by which the device operates, as Judge Rich has explained, and is independent of how that configuration is provided. The structure may reside in semiconductor chips and hardwired connections, or be permanently embedded in the electronic form designated read-only memory, or removably embedded in the electronic form designated random-access memory. It is not relevant to section 101 whether the structure is hard-wired or programmed, machine-readable or manually performed, and indeed the means-plus-function style of claim accommodates these alternatives.

Devices that work by way of digital electronics are not excluded from the patent system simply because their mechanism of operation can be represented by mathematical formulae. The output of an electronic device or circuit may be approximated to any required degree as a mathematical function of its current state and its inputs; some devices, such as the transistor, embody remarkably elementary mathematical functions. Principles of mathematics, like principles of chemistry, are "basic tools of scientific and technological work". Benson, 409 U.S. at 67, 93 S.Ct. at 255. Such principles are indeed the subject matter of pure science. But they are also the subject matter of applied technology.

Digital electronic devices implement mathematical manipulations of electronic signals, as chemical structures and reactions implement principles of molecular behavior. An apparatus that is configured to perform specific electronic procedures in accordance with instructions that require numerical measurements and mathematical calculations is no less statutory than any other combination of steps and components.

This view doesn't contain any notion of semantics or semiotics. Sign-vehicle, interpretant and referent are conflated. The judge considers the invention to be solely the physical device. She pays no attention to the semantical relationships.

14 See also the amicus brief (PDF) Microsoft, Phillips and Symantec submitted to the Supreme Court in Bilski vs Kappos. It contains an elaborate story of fictional computer science which concludes with these words:

Purporting to analyze the patent-eligibility of software, as opposed to that of hardware, relies on an illusory distinction. The functionality of any digital device is the product of the same transistor activity, and it is the configuration of the pathways between those transistors that dictates their functionality.

But the distinction is not illusory. The functionality of a computation is determined by the semantics of the symbols. This is not the product of transistor activity. If you examine the brief you will find that the "explanation" doesn't mention semantics. It doesn't mention bits and symbols.

This brief contains a technical error. It is apparent in this quote:

The fantastic variety in which computers are now found can obscure the remarkable fact that every single one is, at its heart, a collection of tiny on-off switches -- usually in the form of transistors. See generally David A. Patterson & John L. Hennessy, Computer Organization and Design (4th ed. 2009); Ron White, How Computers Work (8th ed. 2005). Just as the configuration of gears and shafts determined the functionality of Babbage's computers, it is the careful configuration of these on-off switches that produces the complex and varied functionality of modern computers.

Today, these on-off switches are usually found in pre-designed packages of transistors commonly known as "chips." Thin wafers of silicon, chips can contain many millions of transistors, connected to one another by conductive materials etched onto the chip like a web of telephone lines. They are organized such that they can be turned on or off in patterned fashion, and by this method, perform simple operations, such as turning on every transistor whose corresponding transistor is off in the neighboring group. From these building blocks, mathematical and logical operations are carried out. Patterson & Hennessy, supra, at 44-47 & App. C.

The challenge for the inventor is how to use these transistors (and applying the principles of logic, physics, electromagnetism, photonics, etc.) in a way that produces the desired functionality in a useful manner. Computer programming is an exercise in reductionism, as every feature, decision, and analysis must be broken down to the level of the rudimentary operations captured by transistors turning on and off. This reductionism is matched by the detail with which transistors must be configured and instructed to carry out the thousands or millions of operations required by the process.

ENIAC -- the first general-purpose electronic digital computer, functioning at the midpoint of the Twentieth Century -- could take days to program, with operators physically manipulating the switches and cables. Patterson & Hennessy, supra, at 1.10.

Fortunately, this is no longer the case. Transistors, packaged onto silicon chips, permit electronic manipulation of the pathways between them, allowing those pathways to be altered to implement different processes without direct physical manipulation. The instructions for this electronic reconfiguration are typically expressed in computer software.

A picture is worth a thousand words. You may see here a picture of how the early ENIAC was programmed. It shows the plug board where wires were manually connected. An ENIAC programmer had to pull out the wires from the old program and insert different wires for the new program. This operation actually configured a new circuit.

You may compare the ENIAC with this picture of a modern integrated circuit viewed through a microscope. Another similar picture is here. The ribbon-like structures are the pathways between transistors mentioned in the brief. Where are the transistors? They are not visible on these pictures but their locations may be identified. Pathways may intersect. Intersections are visible on the pictures. The pathways are superimposed one on top of the other at the points of intersection. The transistors are located where the intersecting pathways are in contact. As you can see, pathways on an integrated circuit can't be disconnected and reconnected like an ENIAC plugboard. They are permanently laid out on the chip surface.

When discussing the configuration of pathways between transistors the brief is incorrectly conflating two different notions of technology. The first one is the electric conductors between the electronic components. The other is whether or not current actually flows in the conductors. These two notions serve two different purposes. The physical configuration of the conductors connects components together. It creates the pathways where the current may flow. But transistors are devices which apply voltages to a conductor. If the voltage is zero, no current flows and this is usually interpreted as the bit 0. If the voltage is not zero the current flows and this is usually interpreted as the bit 1. In both scenarios a bit of data is represented by the voltage. The function of connecting components together is not the same thing as representing a bit of data.

The brief gives the impression that modern computers are programmed by reconfiguring the electrical conductors like an early ENIAC. But an integrated circuit doesn't allow to reconfigure the conductors, Modern computers are programmed by giving a program as input to the instruction cycle. This is another concept which isn't mentioned in the brief but must be present in a technically correct explanation.

The brief gives the impression that transistor activity is equivalent to the configuration of conductors. Transistors don't do that. Transistors control the voltages which are used to represent bits. The activity of the transistors is the manipulation of the bits.

But the fundamental problem with the brief is not the technical error. It is that it misrepresents the nature of the invention in software. It makes believe that the distinction between a software patent and a hardware patent is illusory. They achieve this result by never using any word which may indicate the presence of symbols and their semantics. An unwary reader may never notice that a complete and accurate explanation of software requires these notions.

15 Judge Rich wrote a dissenting opinion in In re Johnston (September 19, 1974) (emphasis in the original):

I am quite familiar with the legal doctrine that a new program makes an old general purpose digital computer into a new and different machine. This court has been through that many times and I am not denying the validity of this principle -- which partakes of the nature of a legal fiction when it comes to drafting claims. My problem is that, knowing the invention to be a new program, I must decide whether it is patentable in any claimed form in view of Benson, whether claimed as a machine, a "machine system," or otherwise.

16 See [Collins 2010] p. 1419 (p. 41 in the PDF)

17 See [Collins 2010] p. 1421 (p. 43 in the PDF)

18 See [Collins 2010] p. 1430 (p 52 in the PDF)

19 See [Collins 2010] p. 1443 (p 65 in the PDF)

20 Collins reports that the Morse code has been patented and the claim has been upheld by the Supreme Court in O'Reilly vs Morse. See [Collins 2010] footnote 251 p. 1426 (p 48 in the PDF)